Sześcian anonim: Sześcian o krawędzi długości a=3 przecięto płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do płaszczyzny podstawy pod kątem α=30 stopni. Oblicz pole otrzymanego przekroju. b) Rozwiąż to samo równanie w przypadku ogólnym, przyjmując, że α należy do przedziału (0,90 stopni). W punkcie a) wyjdzie chyba 3 pierwiastki z 3. Prosiłbym o pomoc z podpunktem b).

anonim: Byłby ktoś w stanie z tym pomóc?

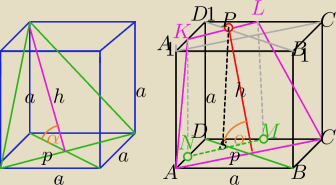
Mila: 1) p=a√2

	a
tgα=
	0.5√2a

tgα=√2 α₀≈54.74^o Dla α∊(0,α₀> przekrój jest trójkątem równoramiennym 2) dla α∊(α₀, 90^o) przekrój jest trapezem równoramiennym 3) dla α=90^o przekrój jest prostokątem (ACC₁A₁) spróbujesz sam (2) ?

anonim: Dzięki, można prosić o rozwiązania? Chciałbym sobie tylko sprawdzić wyniki.

Mila: Sporo pisania. (2) O− punkt przecięcia przekątnych

	|AC|+|KL|
PACLK=		*h
	2

|MN|=|KL| 1) W ΔPSO:

	a		a
sinα=		⇔h=
	h		sinα

	a
tgα=		⇔|OS|=a*ctgα
	|OS|

2)

	1
|DS|=		a√2−a*ctgα
	2

ΔMND∼ΔACD⇔

MN		a√2
	=		⇔|MN|=2*|DS|
DS		12a√2

|MN|=a√2−2actgα

	a√2+a√2−2actgα		a
PACLK=		*
	2		sinα

	a2(√2−ctgα
PACLK=
	sinα

========================

anonim: Dzięki za pomoc

Mila: