Równanie liczb zespolonych + płaszczyzna Rodzisława: Rownanie liczb zespolonych i zapisac na plaszczyznie : (2z)³ = (√2/2 − √2/2 i)² Potrzeba na jak najszybciej! Próbowałam zrobić z postaci wykładniczej liczb zespolonych, ale wychodzą mi jakieś bzdury (lub nie) r= 1/2 α=π/2+2kπ/3 z0=1/2(eⁱπ/2) z1=1/2(eⁱπ7/6) z2=1/2(eⁱπ11/6) Jak przejdę na algebraiczną to wyjchodzi mi: z0=1/2 i z1=(−√3/4)−1/4 i z2=(√3/4)−1/4 i

Rodzisława: r − moduł

jc:

	1−i
(2z)3=(		)2 = −i
	√2

	√3+i		−√3+i
z = i/2,		,
	4		4

jc: Nie rozumiem, dobrze masz, tylko dlaczego tak dziwnie zapisałeś liczbę po prawej stronie? Bardzo dziwnie wygląda to 2/√2. przecież to po prostu 1/√2.

√2		√2		1 − i
	−		i =
2		2		√2

,

Rodzisława: Taka postać była od samego początku po prostu. I z tego od razu podniosłam do kwadratu to po prawej stronie i tak samo wyszło mi "−i" Czyli gdybym teraz chciała to zaznaczyć na płaszczyźnie to jak to ma wyglądać? Mam znaleźć sobie te punkty na oko i poprowadzić do nich strzałki z początku układu współrzędnych?

Rodzisława: Czy oprócz z postaci wykładniczej liczb zespolonych, dałoby radę zrobić to innym sposobem? Bo akurat do tego doszłam dopiero po jakimś czasie, jak nie wychodziło mi nic z postaci algebraicznej

jc: Każdym sposobem.

Rodzisława: Tylko, że wychodzą okropne liczby No nic, dziękuję za sprawdzenie

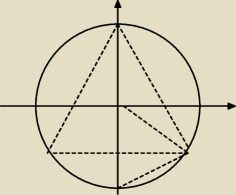
jc: Teraz zauważyłem, że przed i wpisałem omyłkowo plusy zamiast minusów. Pierwiastki mogłaś odczytać z rysunku. Koło o promieniu 1/2, u góry i/2, u dołu (±√3 − i)/4. Duży (mały też) trójkąt jest równoboczny. Mały trójkąt dorysowałem, aby było lepiej widać współrzędne. Wystarczy pamiętać, że wysokość trójkąta równobocznego o podstawie a (u nas 1/2) wynosi a √3/2.

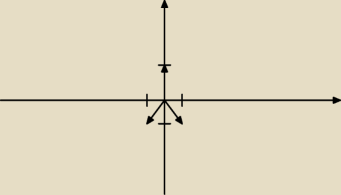
Rodzisława: Czyli jak powinnam zaznaczyć to na płaszczyźnie? Tak jak ty? Trójkąt wpisany w okrąg i ten trójkąt linią przerywaną a okrąg ciągłą? Czy po prostu :