ostrosłup Metin: Oblicz objętość ostrosłupa prawidłowego czworokątnego, w którym wszystkie krawędzie mają długość 3a. Oblicz ctg kąta zawartego między sąsiednimi ścianami bocznymi.

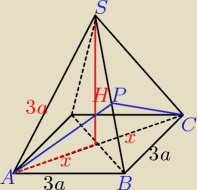
Basia: (2x)² = (3a)²+(3a)² 4x² = 9a²+9a² 4x²=18a²

	18		9
x2 =		a2 =		a2
	4		2

	√18		3√2
x =		a =		a
	2		2

x²+H² = (3a)²

9
	a2+H2 = 9a2
2

	9
H2 = 9a2−		a2
	2

	9
H2 =		a2
	2

	3
H =		a
	√2

	3√2
H =		a
	2

	3√2		27√2
V = (3a)2*H = 9a2*		a =		a3
	2		2

odcinki AP i CP są wysokościami ścian bocznych są więc prostopadłe do BS w punkcie P czyli szukanym kątem jest ∡APC

	3a√3
AP=CP =
	2

AC = 2x = 3√2a z tw.cosinusów AC² = AP²+CP²−2AP*CP*cosα

	9*3*a2		9*3a2		3a√3		3a√3
9*2a2 =		+		− 2*		*		*cosα
	4		4		2		2

	2*27		2*9*3
18a2 =		a2 −		a2*cosα /*4 /:a2
	4		4

72 = 54 − 54cosα 54 cosα = 54−72 54cosα=−18 cosα=−¹⁸₅₄=−⁹₂₇ = −¹₃ sin²α+cos²α=1 sin²α+¹₉=1 sin²α=⁸₉

	2√2
sinα=
	3

	cosα		1		3		1		√2
ctgα=		= −		*		= −		= −
	sinα		3		2√2		2√2		4