Łatwa suma z dwumianem Newtona Maks:

	51 0		51 1		51 25
Oblicz:		+		+ ... +

Maciek: 2⁵⁰

Mila:

	51 n
∑(n=0 do 51)		=251

	1
S=		*251=250
	2

Maks: @Mila, czy mogłabyś wytlumaczyc mi po krótce Twoje rozwiązanie?

Mila: Może na mniejszej potędze:

	5 0		5 1		5 2		5 3		5 4		5 5
(1+1)5=		+		+		||+		+		+		=25

ale :

5 0		5 5
	=

5 1		5 4
	=

5 2		5 3		n k		n n−k
	=		ze wzoru		=

W takim razie :

	5 0		5 1		5 2
25=2*(		+		+		)

stąd :

	5 0		5 1		5 2		25
(		+		+		)=		=16
							2

L=1+5+10=P Zatem :

	51 0		51 1		51 25
251=2*(		+		+...........+.		)

Maks: @Mila, dzięki wielkie, teraz już rozumiem! Skoro udało mi się zająć Twoją uwagę, to czy mogłabyś zerknąć jeszcze na takie zadanko? Napisz równanie paraboli o ognisku w punkcjie (5,0) i kierownicy x=7. Z góry dziękuję!

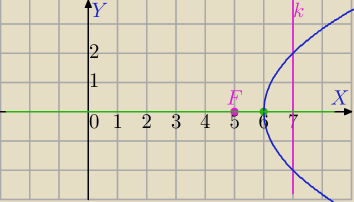
Mila: F(5,0)− ognisko paraboli x=7− równanie kierownicy 1) Oś symetrii paraboli przechodzi przez ognisko i jest prostopadła do kierownicy⇔ y=0 oś symetrii 2) odległość kierownicy od ogniska równa 2⇔p=2 Ognisko i wierzchołek paraboli leżą zawsze na osi symetrii paraboli. Wierzchołek paraboli leży dokładnie w połowie odległości między ogniskiem a kierownicą. (y−y₀)²=2p(x−x₀) W=(6,0) (y−0)²=2*2(x−6) y²=4(x−6)

Maks: @Mila, jeszcze raz uprzejmie dziękuję za pomoc!

Mila: Niestety jest błąd. Parabola nie może przecinać kierownicy ( zastanów się dlaczego) y²=−4(x−6) Teraz z definicji wyznaczymy równanie : Parabola jest zbiorem wszystkich punktów P(x,y), których odległości od kierownicy są równe odległościom od ogniska. F(5,0)− ognisko paraboli x=7− równanie kierownicy √(x−5)²+(y−0)²=|x−7| x²−10x+25+y²=x²−14x+49⇔ y²=−4x+24⇔ y²=−4*(x−6) ===========

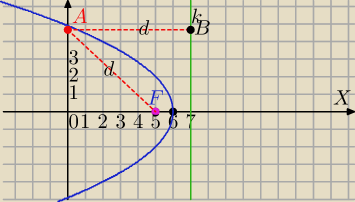
Mila: A=(0,√24 |AF|=7=|AB|