1)
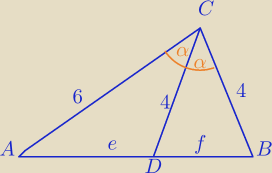
6*4*sinα+4*4*sinα=6*4*sin(2α)
40sinα=24sin2α
5sinα=3*2sinα*cosα
5=6cosα
| 5 | ||
cosα= | ||
| 6 |
| 25 | ||
2) sin2α=1− | ||
| 36 |
| 11 | √11 | |||
sin2α= | ⇔sinα= | |||
| 36 | 6 |
| 5 | √11 | |||
3) 2*sinα*cosα=2* | * | |||
| 6 | 6 |
| 5√11 | ||
sin(2α)= | ||
| 18 |
| 1 | ||
4) PΔ= | *6*4*sin(2α) | |
| 2 |
| 5√11 | 10√11 | |||
PΔ=12* | = | |||
| 18 | 3 |
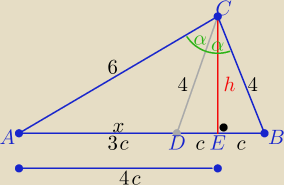3 sposób
z twierdzenia o dwusiecznej
| x | 2c | ||
= | ⇒ x=3c | ||
| 6 | 4 |
| 4 | ||
z tw. Pitagorasa h2=16−c2 i h2=36−16c2 ⇒ c2= | ||
| 3 |
| 2 | 2√11 | |||
to c= | i h= | |||
| √3 | √3 |
| 1 | 1 | 2 | 2√11 | 10√11 | ||||||
P(ABC)= | *5c*h= | *5 | * | = | ||||||
| 2 | 2 | √3 | √3 | 3 |