Uzasadnij, że w przedziale ⟨−2,5⟩ funkcja f przyjmuje największą wartość Boczek: Funkcja kwadratowa f przyjmuje w przedziale ⟨0,3⟩ największą wartość dla argumentów 0 i 3. Uzasadnij, że w przedziale ⟨−2,5⟩ funkcja f przyjmuje największą wartość dla argumentów −2 i 5. Myślałem, żeby porównać średnią arytmetyczną punktów: −2+5/2==0+3/2 I z tego wynika, że punkty są symetryczne(niekoniecznie z mojego "równania") względem osi symetrii paraboli, ale nie mam pojęcia jak to zapisać.

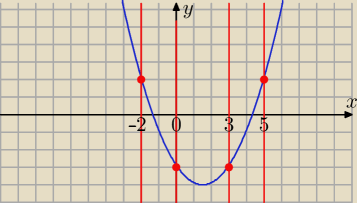
Bogdan: To jest ilustracja tego zagadnienia

Boczek: Do tego doszedłem sam, mam problem opisania tego

Bogdan: Zapisać można tak: Jeśli parabola dla dwóch wartości przyjmuje tę samą wartość: f(a) = f(b),

	a + b		(a − r) + (b + r)
to oś symetrii x =		=		, stąd f(a − r) = f(b + r).
	2		2