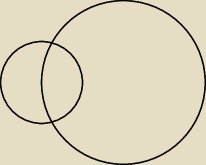
Oblicz pole części wspólnej kół o różnych promieniach. rexar123499: Środek lewego koła leży na krawędzi prawego koła. Lewe koło ma promień 2, a prawe ma promień 3. Muszę policzyć pole części wspólnej tych kół. Przepraszam za słaby rysunek, ale piszę z komórki, bo bardzo potrzebuję tego zadania.

rexar123499: Proszę

Janek191: Narysuj wspólną cięciwę tych okręgów, a następnie pola odcinków kół. Szukane pole jest sumą obliczonych pól odcinków kół.

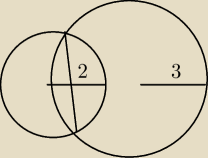
rexar123499: To są jedyne dane do tego zadania. Nie mam żadnych informacji o kątach ani nic. Jak mam to zrobić?

Janek191: Kąty trzeba wyliczyć − tw. kosinusów

rexar123499: I tu się pojawia problem, bo te zadanie jest niby na poziomie gimnazjum... Tw. Cosinusów znam, jednak czy nie ma innej metody?

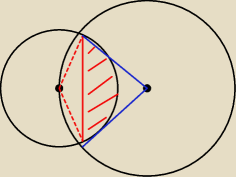
kochanus_niepospolitus: zaznaczoną część wyliczasz ze wzoru na wycinek koła (o r=2) Drugą część analogicznie, ale wykorzystując ten wzór dla dużego okręgu.

rexar123499: kochanus_niepospolitus Jak mam użyć tego wzoru skoro nie znam kąta między ramionami (przeczytaj koment wyżej )

rexar123499: Po prostu czy isnieje metoda gimnazjalna, bo znajomy miał to na sprawdzianie w gimnazjum i tak siedzę i myślę...

g:

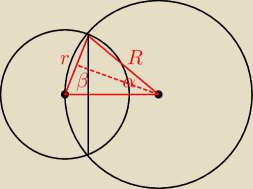
	r
sin(α/2) =		α = 2 arcsin(r/2R)
	2R

β = 90−α/2

	R2*2α		R2*sin(2α)
Wzór na jeden z tych wycinków:		−
	2		2