TRAPEZ TRAPEZ: W trapezie ABCD, AB || DC oraz |AB|>|DC|. Na podstawie DC wybrano punkt M w taki sposób, że |DM|MC|=9:16. Prosta AM przecina przedłużenie ramienia BC w punkcie E. Punkt P jest punktem wspólnym przekątnej BD i odcinka AE. Wykaż, że jeśli AP=ME, to PM=0,25AP

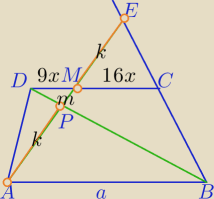Mila: x− wspólna miara, x>0 |AP|=|ME|=k

	k		2k+m
1) ΔABE∼ΔMCE⇔		=
	16x		a

ka=16x*(2k+m) 2) ΔDMP∼ΔAMP⇔

9x		a		9x		a
	=		⇔		=
m		AP		m		k

m*a=9x*k 3)

k*a		16x*(2k+m)		k		16*(2k+m)
	=		⇔		=		⇔
m*a		9x*k		m		9k

16m²+32k*m−9k²=0, m>0 Δ=1600k²

	−32k−40k		−32k+40k		8k
m=		<0 lub m=		=
	32		32		32

	1		1
m=		k=		|AP|
	4		4

=========