xd help me pls: W czworokącie wypukłym ABCD wpisanym w okrąg miary dwóch kolejnych kątów wynoszą L oraz 90+L, gdzie L∊(0,90). Wykaż że jeśli sin(L+45) = 2√2/3 to suma długości przekątnych tego czworokąta jest równa 8/3 R, gdzie R to promień okregu opisanego na tym czworokącie. Sam zrobiłem tyle: Kolejne kąty to L, 90+L, 180−L, 90−L. Suma naprzeciwległych bokow jest równa. Sinus to około 0,9428

Bogdan: zastosuj twierdzenie sinusów

TRAPEZ: ale nie mam żadnego boku

TRAPEZ: są kąty tylko

kochanus_niepospolitus:

	przekątna1
2R =
	sinL

	przekątna2
2R =
	sin(L+90)

przekątna₁ + przekątna₂ = 2R(sinL + sin(L+90))

	2L + 90		90
przekątna1 + przekątna2 = 2R*2sin(		)cos(		)
	2		2

przekątna₁ + przekątna₂ = 2R*2*sin(L+45^o)cos(45^o)

	2√2		√2
przekątna1 + przekątna2 = 2R*2*		*
	3		2

	8
przekątna1 + przekątna2 =		R
	3

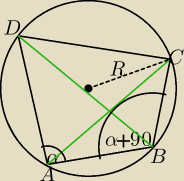
Bogdan: e = |AC|, f = |BD|

	e		f
z tw. sinusów:		= 2R,		= 2R
	sin(90 + α)		sinα

e = ..., f = ...., e + f = .....

TRAPEZ: ok juz mam dzieki