zad Maciek: Mamy 15 monet jednozłotowych, które układamy przypadkowymi stronami w trójkat równoboczny (kładąc w pierwszym rzedzie 5 monet, w drugim 4, potem 3, 2 oraz 1 ). Prawdopodobieństwo zdarzenia, że środki pewnych trzech monet leżących tą sama stroną do góry są wierzchołkami trójkąta równobocznego jest

g: Toż to chyba zdarzenie pewne.

Maciek: ile jest równe

Czarek: No jak pewne? Przecież układasz przypadkowo wiec narozniki moga byc rózne. Np orzel reszka orzel

Czarek: Przykładowy trójkąt spełniający warunek i nie spelniajacy

Adamm: drugi też spełnia nie jest powiedziane że monety muszą przylegać

Czarek: Chociaż w sumie w drugim trojkacie jest mniejszy trojkat o 3 czarnych Wierzchołkach, ale nie wiem mamy rozpatrzyc wszystkie składowe trójkąty czy tylko ten główny, jeśli wszystkie to masz rację zdarzenie będzie 100% pewne

Czarek: Zgadza się ja brałem pod uwagę wierzchołki tego głównego trójkąta tylko więc sorry za pomylke

Maciek: czemu 100%?

kochanus_niepospolitus: Spostrzeżenie 1: W jednej linii NIE MOGĄ pojawić się trzy tego samego koloru. (5,1 ; 4,1 ; 3,1 są czarne) Bo wtedy w rzędzie obok konieczne są dwie innego koloru (5,2 ; 4,2 są niebieskie) Co zmusza nas do wstawienia pierwszego koloru na miejsce (5,3) co daje nam trójkąt równoboczny złożony z 6 monet

Czarek: Tak czy inaczej z tych punktow da się utworzyć 26(?) różnych równobocznych trójkątów nie jest możliwe żeby wszystkie kombinacje miały jednoczesnie 3 różne wierzchołki kiedy dysponujemy tylko 2 kolorami. Dla pewności nawet rzucałem monetami i na 10 prób zawsze znalazłem przynajmniej jeden trójkąt

Czarek: Tak czy inaczej z tych punktow da się utworzyć 26(?) różnych równobocznych trójkątów nie jest możliwe żeby wszystkie kombinacje miały jednoczesnie 3 różne wierzchołki kiedy dysponujemy tylko 2 kolorami. Dla pewności nawet rzucałem monetami i na 10 prób zawsze znalazłem przynajmniej jeden trójkąt

kochanus_niepospolitus: Spostrzeżenie 2 −−− wymaga to już sprawdzenia różnych przypadków ... Nie mogą być dwa jednakowego koloru w jednej linii na grzbiecie. Więc zostaje nam jedynie sytuacja gdy są 'na przemian' a wtedy powstanie trójkąt z niebieskich. Natomiast zagadką pozostaje jak to matematycznie udowodnić

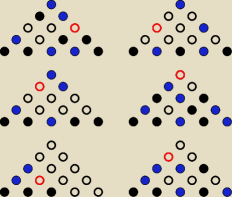
kochanus_niepospolitus: To są wszystkie możliwości −−− czerwone miejsce oznacza, że cokolwiek nie położymy mamy albo niebieski albo czarny trójkąt. Rozpatrzyłem wszystkie możliwe rozłożenia kolorów na dolnej krawędzi dużego trójkąta po czym wrzucałem kolejne monety tylko tam gdzie trzeba było, aby przeszkodzić w powstaniu trójkąta o tym samych wierzchołkach.

kochanus_niepospolitus: Innymi słowy −−− najpierw zapełniałem cały dolny rząd, a później patrzyłem 'co się będzie dalej działo'