zad Maciek: Dany jest trójkąt prostokątny ABC, w którym AB jest przeciwprostokątną o długości a. Na prostej zawierającej bok AC wybrano punkt D w taki sposób, że C jest środkiem odcinka AD. Niech f (α) oznacza pole koła wpisanego w trójkąt ABD, gdzie α jest miarą kąta BAC Wyznacz f(α)

iteRacj@: Mila możesz wytłumaczyć, czemu pole koła wpisanego w trójkąt ABD jest równe h*b? zupełnie tego nie wiem

Mila: Przepraszam, obliczyłam pole ΔADB. Zaraz po kolacji dokończę zadanie, coś dzisiaj niedokładnie czytam treści zadań. Dziękuję iteRacjo, nomen omen. Pozdrawiam

iteRacj@: żaden 'omen' pozdrawiam

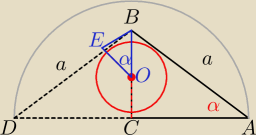
kochanus_niepospolitus: niebieski trójkąt (OBE) jest podobny do trójkąta ABC (podobieństwo kkk). Stąd α

	h
sinα =		−> h = a*sinα
	a

h = |CO| + |OB| = r + x

	|OE|		r		r
cosα =		=		−> x =
	|OB|		x		cosα

czyli:

	r		cosα+1		asinα(cosα+1)
a*sinα = r +		⇔ r*		= asinα ⇔ r =
	cosα		cosα		cosα

	asinα(cosα+1)
f(α) = π(		)2
	cosα

Maciek:

	asinαcosα
błąd r=
	cosα+1

kochanus_niepospolitus: fakt

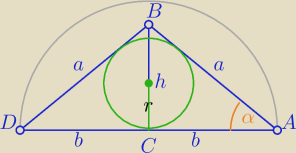
Mila: II sposób h=a*sinα b=a*cosα

	1		1
1) PΔADB=		*2b*h=		a2sin(2α)
	2		2

2) P_ΔADB=p*r=(a+b)*r=(a+acosα)*r

	1
a*(1+cosα)*r=		a2sin(2α}
	2

	asin(2α)
r=
	2*(1+cosα)

	a2sin2(2α)
Po=f(α)=π*
	4*(1+cosα)2

==========================

iteRacj@: i już wszystko jasne, dziękuję