rozwiązań równania |x2 – 2|x| – 3| = |m| – 1
Pola:
Naszkicuj wykres funkcji y = |x2 – 2|x| – 3|, a następnie, korzystając z tego wykresu, określ
liczbę
rozwiązań równania |x2 – 2|x| – 3| = |m| – 1 w zależności od wartości parametru m (m Î R).
Naszkicuj wykres funkcji y = g(m) wyrażającej liczbę rozwiązań tego równania w zależności
od wartości parametru m.
Naszkicowałam wykres funkcji, ale nie rozumiem części |m| – 1 oraz wykresu y = g(m)
23 lis 22:20
Pola: y=3x|x2 − 2|
23 lis 22:21
Eta:
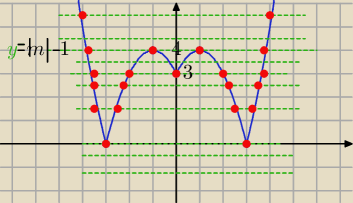
zad 1/
f(x)−−− wykres
y=|m|−1
0 rozwiązań dla
y<0 ⇒ |m|−1<0 ⇒ m∊(−1,1)
2 rozwiązania dla
y=0 lub
y>4
|m|=0 lub |m|>5
m=0 lub m∊(−
∞, −5)U (5,
∞)
4 rozwiązania dla |m|−1=4 lub |m|−1∊(0,3)
m=5 lub m= −5
lub ( |m|−1>0 i |m|−1<3) ⇒m∊(−4,−1)U(1,4)
5 rozwiązań dla |m|−1=3 ⇒ m=−4 lub m= 4
23 lis 23:07
Mila:
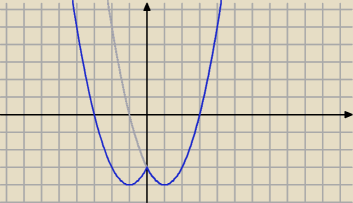
|x
2 – 2|x| – 3| = |m| – 1
1)
g(x)=x2−2x−3
2) symetria względem OY wykresu z prawej strony OY⇒otrzymujemy wykres :
h(x)=x2−2|x|−3
3) symetria względem OX tej części wykresu leżącej pod osią OX⇒
f(x)= |x2 – 2|x| – 3|
narysuję w nowym wątku
23 lis 23:11
Pola: Dziękuję za tak pięknie opisaną pomoc, to forum jest pełne miłych ludzi

23 lis 23:15
Eta:
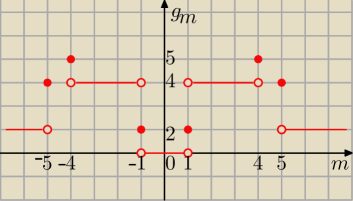
poprawiam
2 rozwiązania dla
y=0 ⇒ |m|−1=0⇒ m=1 lub m= −1 lub ...... ( dalej już jest dobrze
I narysowałam wykres
g(m) ilości rozwiązań
23 lis 23:17
Eta:
No to już nie przeszkadzam

Pozdrawiam
Milę 
23 lis 23:19
Pola: Dziękuje, jeszcze raz!

23 lis 23:24
Eta:
Na zdrowie .... łap


23 lis 23:25
Mila:
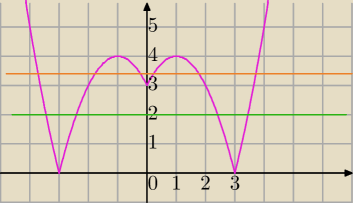
[F[f(x)= |x
2 – 2|x| – 3|
f(x)=|m|−1
1) |m|−1<0 brak rozwiązań
|m|<1⇔
m∊(−1,1)
2)
|m|−1=0 ⇔
m=1 lub m=−1 dwa rozwiązania
3)
0<|m|−1<3 /+1
cztery rozwiązania⇔
1<|m|<4⇔|m|>1 i |m|<4⇔
{m<−1 lub m>1] i m∊(−4,4)⇔
m∊(−4,−1)∪(1,4) narysuj sobie na osi liczbowej
4) |m|−1=3 pięć rozwiązań
|m|=4⇔
m=−4 lub m=4
5)
3<|m|−1<4 6 rozwiązań
4<|m|<5⇔|m|>4 i |m|<5
[m<−4 lub m>4] i m∊(−5,5)⇔
m∊(−5,−4) ∪(4,5)
6)
|m|−1=4 cztery rozwiązania
m=−5 lub m=5
7) |m|−1>4 dwa rozwiązania
|m|>5
m<−5 lub m>5
23 lis 23:33
Mila:
Pozdrawiam

23 lis 23:35
Mila:
No to zdublowane rozwiązanie, długo pisałam

23 lis 23:49
 Naszkicuj wykres funkcji y = |x2 – 2|x| – 3|, a następnie, korzystając z tego wykresu, określ
liczbę
rozwiązań równania |x2 – 2|x| – 3| = |m| – 1 w zależności od wartości parametru m (m Î R).
Naszkicuj wykres funkcji y = g(m) wyrażającej liczbę rozwiązań tego równania w zależności
od wartości parametru m.
Naszkicowałam wykres funkcji, ale nie rozumiem części |m| – 1 oraz wykresu y = g(m)
Naszkicuj wykres funkcji y = |x2 – 2|x| – 3|, a następnie, korzystając z tego wykresu, określ
liczbę
rozwiązań równania |x2 – 2|x| – 3| = |m| – 1 w zależności od wartości parametru m (m Î R).
Naszkicuj wykres funkcji y = g(m) wyrażającej liczbę rozwiązań tego równania w zależności
od wartości parametru m.
Naszkicowałam wykres funkcji, ale nie rozumiem części |m| – 1 oraz wykresu y = g(m)
 zad 1/
f(x)−−− wykres
y=|m|−1
0 rozwiązań dla y<0 ⇒ |m|−1<0 ⇒ m∊(−1,1)
2 rozwiązania dla y=0 lub y>4
|m|=0 lub |m|>5
m=0 lub m∊(−∞, −5)U (5,∞)
4 rozwiązania dla |m|−1=4 lub |m|−1∊(0,3)
m=5 lub m= −5
lub ( |m|−1>0 i |m|−1<3) ⇒m∊(−4,−1)U(1,4)
5 rozwiązań dla |m|−1=3 ⇒ m=−4 lub m= 4
zad 1/
f(x)−−− wykres
y=|m|−1
0 rozwiązań dla y<0 ⇒ |m|−1<0 ⇒ m∊(−1,1)
2 rozwiązania dla y=0 lub y>4
|m|=0 lub |m|>5
m=0 lub m∊(−∞, −5)U (5,∞)
4 rozwiązania dla |m|−1=4 lub |m|−1∊(0,3)
m=5 lub m= −5
lub ( |m|−1>0 i |m|−1<3) ⇒m∊(−4,−1)U(1,4)
5 rozwiązań dla |m|−1=3 ⇒ m=−4 lub m= 4
 |x2 – 2|x| – 3| = |m| – 1
1) g(x)=x2−2x−3
2) symetria względem OY wykresu z prawej strony OY⇒otrzymujemy wykres :
h(x)=x2−2|x|−3
3) symetria względem OX tej części wykresu leżącej pod osią OX⇒
f(x)= |x2 – 2|x| – 3|
narysuję w nowym wątku
|x2 – 2|x| – 3| = |m| – 1
1) g(x)=x2−2x−3
2) symetria względem OY wykresu z prawej strony OY⇒otrzymujemy wykres :
h(x)=x2−2|x|−3
3) symetria względem OX tej części wykresu leżącej pod osią OX⇒
f(x)= |x2 – 2|x| – 3|
narysuję w nowym wątku

 poprawiam
2 rozwiązania dla y=0 ⇒ |m|−1=0⇒ m=1 lub m= −1 lub ...... ( dalej już jest dobrze
I narysowałam wykres g(m) ilości rozwiązań
poprawiam
2 rozwiązania dla y=0 ⇒ |m|−1=0⇒ m=1 lub m= −1 lub ...... ( dalej już jest dobrze
I narysowałam wykres g(m) ilości rozwiązań
 Pozdrawiam Milę
Pozdrawiam Milę 



 [F[f(x)= |x2 – 2|x| – 3|
f(x)=|m|−1
1) |m|−1<0 brak rozwiązań
|m|<1⇔m∊(−1,1)
2)
|m|−1=0 ⇔m=1 lub m=−1 dwa rozwiązania
3)
0<|m|−1<3 /+1
cztery rozwiązania⇔
1<|m|<4⇔|m|>1 i |m|<4⇔
{m<−1 lub m>1] i m∊(−4,4)⇔
m∊(−4,−1)∪(1,4) narysuj sobie na osi liczbowej
4) |m|−1=3 pięć rozwiązań
|m|=4⇔m=−4 lub m=4
5)
3<|m|−1<4 6 rozwiązań
4<|m|<5⇔|m|>4 i |m|<5
[m<−4 lub m>4] i m∊(−5,5)⇔
m∊(−5,−4) ∪(4,5)
6)
|m|−1=4 cztery rozwiązania
m=−5 lub m=5
7) |m|−1>4 dwa rozwiązania
|m|>5
m<−5 lub m>5
[F[f(x)= |x2 – 2|x| – 3|
f(x)=|m|−1
1) |m|−1<0 brak rozwiązań
|m|<1⇔m∊(−1,1)
2)
|m|−1=0 ⇔m=1 lub m=−1 dwa rozwiązania
3)
0<|m|−1<3 /+1
cztery rozwiązania⇔
1<|m|<4⇔|m|>1 i |m|<4⇔
{m<−1 lub m>1] i m∊(−4,4)⇔
m∊(−4,−1)∪(1,4) narysuj sobie na osi liczbowej
4) |m|−1=3 pięć rozwiązań
|m|=4⇔m=−4 lub m=4
5)
3<|m|−1<4 6 rozwiązań
4<|m|<5⇔|m|>4 i |m|<5
[m<−4 lub m>4] i m∊(−5,5)⇔
m∊(−5,−4) ∪(4,5)
6)
|m|−1=4 cztery rozwiązania
m=−5 lub m=5
7) |m|−1>4 dwa rozwiązania
|m|>5
m<−5 lub m>5

