Geometria
Dawid: Witam mam problem z takim zadaniem nie wiem jak się za nie zabrać "Ściana boczna ostrosłupa
prawidłowego trójkątnego jest nachylona do płaszczyzny jego podstawy
pod takim kątem, że sin alfa=2/5 . Promień okręgu wpisanego w podstawę jest równy 2√3. Wyznacz
objętość ostrosłupa."
23 lis 07:28
Jerzy:
Do objętości tej bryły potrzebujesz znać pole podstawy i jej wysokość.
Mając promieć okręgu wpisanego w podstawę łatwo wyliczysz wysokość podstawy
i jej krawędź. Pozostaje wysokośc bryły, a tą obliczysz ze związków trygonometrycznych
w trójkącie prostokątnym utworzonym przez wysokość bryły, 1/3 wysokości podstawy i
wysokość ściany bocznej.
23 lis 07:59
Eta:
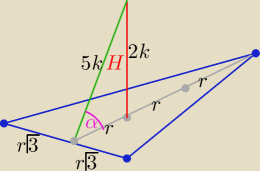
r=2
√3
P
p=r
√3*3r= 3r
2√3 ⇒
Pp= 36√3
| | 2√7 | |
r=√25k2−4k2= √21k ⇒ 2√3=k*√3*√7 ⇒ k= |
| |
| | 7 | |
| | 1 | |
V= |
| *Pp*H=............ |
| | 3 | |
23 lis 20:01
 r=2√3
Pp=r√3*3r= 3r2√3 ⇒ Pp= 36√3
r=2√3
Pp=r√3*3r= 3r2√3 ⇒ Pp= 36√3