monotnicznosc funkcji Misiek: Witam, potrzebuje zbadać monotoniczność funkcji na podstawie definicji: 1) x²+6x−7 2) x/(1+x) 3) sinx+2x < to jest chyba najtrudniejsze To pierwsze robiłem tak: f(x1)−f(x2) = x₁²+6x₁−7−7−x₂²−6x₂+7 = ..... = (6(x₁+x₂))(x₁−x₂) Czyli to działąnie wychodzi ujemne, czyli funkcja jest rosnąca i tyle, nie ma zadnych przedziałów ani nic?

Misiek: Tam niechąco dwa razy siódemkę napisałem.

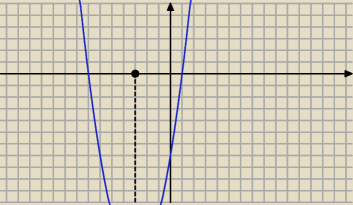
Janek191: 1) Źle − to jest funkcja kwadratowa

	−6
p =		= − 3
	2

f ↘ dla x < − 3 i f ↗ dla x > − 3 Patrz też wykres

Misiek: No wlasnie, to mi nie grało, ale w takim razie czemu tamta wlasnosc nie zachodzi? ze x₁<x₂ i f(x₁)−(x₂)<0 dla rosnacej?

Misiek: 1) Kiedy wiec mam sie stosowac do tej definicji? 2) Dal by rade ktos zrobic tamte 2 przyklady?

Misiek: refresh

iteRacj@: x₁²+6x₁−7−x₂²−6x₂+7 = ..... = (6(x₁+x₂))(x₁−x₂) źle to policzyłeś powinno być f(x₁)−f(x₂) = x₁²+6x₁−7−x₂²−6x₂+7 = (x₁−x₂)² + 6*(x₁−x₂) = (x₁+x₂)*(x₁−x₂) + 6*(x₁−x₂) = (x₁−x₂)*[x₁+x₂ + 6] jeśli x₁<x₂ x₁−x₂<0 a znak różnicy f(x₁)−f(x₂) zależy od znaku (x₁+x₂ + 6) dla x₁+x₂ + 6 >0 czyli x₁+x₂ > −6 funkcja maleje dla x₁+x₂ + 6 <0 czyli x₁+x₂ < −6 funkcja rosnie

Misiek: Aaa, o matko Dzieki wielkie! W 2) powinno być tak? x1/(1+x1)−x2/(1−x2) = x1−x2/(1+x1)(1+x2) Licznik jest ujemny, wiec calosc jest ujemna?

iteRacj@: wczoraj przepisując z kartki zamieniłam miejscami komentarze, poprawiam i uzupełniam: jeśli (x₁<x₂) ⇒ ( f(x₁) < f(x₂) ) to funkcja jest rosnąca czyli z x₁−x₂< 0 ma wynikać że f(x₁)−f(x₂)< 0 tutaj mamy: zał. x₁−x₂<0 a znak różnicy f(x₁)−f(x₂) zależy od znaku wyrażenia (x₁+x₂+6) 1/ dla x₁+x₂+6 <0 czyli x₁+x₂ < −6 mamy f(x₁)−f(x₂)>0 funkcja maleje 2/ dla x₁+x₂+6 >0 czyli x₁+x₂ > −6 mamy f(x₁)−f(x₂)<0 funkcja rośnie

Misiek: Tak, w sumie jak robiełm to drugi raz to u siebie to zrobiłem dobrze i nie zwrocilem uwagi, ze tam jest na odwrót. To jak będzie z tym 2 przykładem, bo jestem wiecej niz pewny ze mam to zle i nie mam. Wiem, ze powinienem jeszcze uwzględnić to, że jeżeli ktorych nawias z mianownika będzie ujemny to liczba będzie dodatania, wiec tutaj na pewno tez będą przedziały, tylko jak to zrobić?

iteRacj@: jak nikt nie napisze wcześniej to napisze to wieczorem, to nie jest bardzo skomplikowane

kochanus_niepospolitus: 2) ''zarys" Zauważamy, że funkcja ta nie jest funkcją ciągłą D_f = R / {1} Należy badać monotoniczność (z definicji) w dwóch oddzielnych przedziałach: 1) x₁, x₂ < 1 2) x₁, x₂ > 1

x		1
	= −1 +
1−x		1−x

	1		1		x2 − x1
x2 − x1 > 0 ⇒ −1 +		− (−1 +		) =		> 0
	1−x2		1−x1)		(1−x2)(1−x1)

(o ile tylko rozpatrujemy tylko jeden z tych dwóch powyższych przypadków)

Misiek: Kompletnie nie rozumiem Twojego sposobu. Dasz radę zrobić jak @iteRacj@ ?

kochanus_niepospolitus: definicja mówi ∀_{x1,x2 ∊Df} x₂ − x₁ > 0 ⇒ f(x₂) − f(x₁) > 0 to funkcja jest rosnąca (analogicznie dla malejącej) I to zastosowałem. Jednak należy zauważyć, że jeżeli x₁ < 1 < x₂ to f(x₂) < f(x₁) Czyli funkcja ta nie jest rosnąca w CAŁEJ SWOJEJ DZIEDZINIE, ale jest rosnąca w przedziałach: (−∞, 1) i (1, +∞)

Misiek: Ale to ja sie zastosowałem także do tego z definicji. Podstawiłem tak jak to zrobiła iteRacj@, z tym ze nie obliczylem dziedziny. Nie rozumiem kompletnie skad masz to: x/1−x=−1+1/1−x co implikuje z tym, ze tego co masz dalej takze nie rozumiem.

kochanus_niepospolitus:

x		−x		1 − x − 1		1−x		−1		1
	= −		= −		= −		−		= −1 +
1−x		1−x		1−x		1−x		1−x		1−x

jest to zwykłe 'przekształcenie' w celu 'zredukowania' ilości x'sów w wyrażeniu.

Misiek: Z tego co napisales ja pod koniec czyt. U{x₂−x₁}{1−x₂)(1−x₁)>0 nic bym nie wywnisokował

Misiek: No dobra, to przeksztalcenie rozumiem, ale nie rozumiem po co tak to wszystko robimy, dlaczego nie mozemy tego zrobić tak jak ja to zrobiłem, ze po prostu podstawiam pod x x₁ lub x₂

kochanus_niepospolitus:

x2 − x1
(1−x2)(1−x1)

I wnioski: licznika: x₂ − x₁ > 0 bo założyliśmy, że x₂>x₁ (patrz definicja) mianownik: a) jeżeli x₁, x₂ < 1 to: (1−x₂) < 0 i (1−x₁) < 0 ... więc iloczyn jest >0 b) jeżeli x₁, x₂ > 1 to: (1−x₂) > 0 i (1−x₁) > 0 ... więc iloczyn jest >0 podsumowując: jeżeli: a) jeżeli x₁, x₂ < 1 to funkcja jest rosnąca b) jeżeli x₁, x₂ > 1 to funkcja jest rosnąca

kochanus_niepospolitus: ale możesz sobie tak podstawić, nikt Ci nie broni i wtedy masz:

x2		x1		x2 − x1
	−		=
1−x2		1−x1		(1−x2)(1−x1)

czyli DOKŁADNIE to samo ... istotne są wnioski, które z tego wyciągniesz, a Ty wyciągasz BŁĘDNY wniosek

Misiek: Ahhh....rozumiem teraz.... dzieki wielkie @kochanus_niepospolitus

Misiek: Tutaj sie rozchodzi caly czas teraz o ta dziedzine, rozumiem.

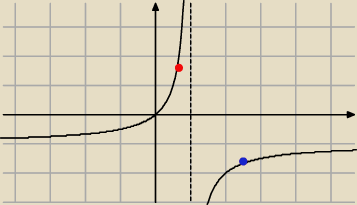
kochanus_niepospolitus: tak wygląda wykres tej funkcji ... teraz widzisz dlaczego należy rozpatrywać ją przedziałami

Misiek: Tak. Choc dlaczego w a) przyjmujesz, że: (1−x2) < 0 i (1−x1) < 0 skoro x₂ i x₁ jest mniejsze od 1, wiec to bedzie dodatnie

Misiek: Oraz skąd wniosek, ze jezeli iloczyny tych dwoch nawiasow jest dodatni, to f. jest rosnąca?

kochanus_niepospolitus: na odwrót miało być się mi pomyliło jak pisałem

kochanus_niepospolitus: iloczyn dwóch LICZB dodatnich jest liczbą dodatnią więc wyrażenie

dodatnia
	> 0 więc f(x2) − f(x1) > 0 .. .więc funkcja rosnąca (patrz
dodatnia*dodatnia

definicja)

Misiek: W sumie prawda. Dzieki wielkie, teraz rozumiem.

Misiek: Choc w liczniku jest liczba ujemna

kochanus_niepospolitus: nie jest ujemna bo z założenia (jakie JA PRZYJĄŁEM) mamy: x₂ − x₁ > 0 (patrz wpis 16:29)

kochanus_niepospolitus: PS. Widzę, że masz w zwyczaju na odwrót to zaznaczać, nie jest to błąd (bo niby czemu), ale proponuję jednak się przyzwyczaić do oznaczenia: x₁ < x₂ (czyli numerujemy od lewej do prawej x'sy) Bo tak raczej robią wykładowcy i może po prostu Ci się gdzieś 'popierdzielić' w trakcie zajęć.

Misiek: No tak, ja caly czas patrzylem, ze własnie x₁<x₂