matematykaszkolna.pl
. Johny: Znajdź liczby zespolone spełniające równanie z3+3z2−z−5=0
22 lis 21:16
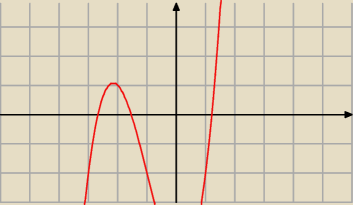
g: rysunekTen wielomian ma trzy pierwiastki rzeczywiste.
22 lis 22:09
Mariusz: z3+3z2−z−5=0 (z3+3z2+3z+1)−4z−6=0 (z+1)3−4z−4−2=0 (z+1)3−4(z+1)−2=0 y=z+1 y3−4y−2=0 y=u+v (u+v)3−4(u+v)−2=0 u3+3u2v+3uv2+v3−4(u+v)−2=0 u3+v3−2+3(u+v)uv−4(u+v)=0
 4 
u3+v3−2+3(u+v)(uv−
)=0
 3 
u3+v3−2=0
 4 
3(u+v)(uv−
)=0
 3 
u3+v3−2=0
 4 
uv−
=0
 3 
u3+v3=2
 4 
uv=
 3 
u3+v3=2
 64 
u3v3=
 27 
 64 
t2−2t+
=0
 27 
 111 
(t−1)2+
=0
 81 
 9−√111i 9+√111i 
(t−
)(t−
)=0
 9 9 
 27−3√111i 27+3√111i 
(t−
)(t−
)=0
 27 27 
 1 
y=
(3√27−3√111i+3√27+3√111i)
 3 
r=√1728
 √111 
θ=arctan(
)
 9 
 2√3 
 √111 
arctan(
)
 9 
 
 √111 
arctan(
)
 9 
 
u=
(cos(
)−isin(
))
 3 3 3 
 2√3 
 √111 
arctan(
)
 9 
 
 √111 
arctan(
)
 9 
 
v=
(cos(
)+isin(
))
 3 3 3 
Sprawdzasz czy para (u,v) spełna układ równań u3+v3=2
 4 
uv=
 3 
Jeśli nie spełnia to tak dobierasz pierwiastki trzeciego stopnia z pierwiastków równania
 64 
t2−2t+
=0
 27 
Jeżeli znajdziesz już jedną taką parę (u,v) spełniającą układ równań u3+v3=2
 4 
uv=
 3 
to pozostałe znajdziesz mnożąc znalezione u oraz v przez pierwiastki trzeciego stopnia z jedynki e2kπi/3
22 lis 22:23
Johny: Super, wielkie dzięki!
22 lis 22:26