Wyznacz pierwiastki zespolone równania Daniel: Mam takie zadanie Wyznacz pierwiastki zespolone równania x³+i=0 A rozwiazanie wyglada tak:

	3		3
x3 = −i = cos		π + isin		π
	2		2

n = 3

	3		3		π		π
x0 = cos		π + isin		π = cos		+ isin		π = i
	6		6		2		2

	7		7		π		π		π
x1 = cos		π + isin		π = cos (π +		) + isin (π +		) = −cos		−
	6		6		6		6		6

	π		−√3		1
isin		=		−		i
	6		2		2

	11		11		π		π		π
x2 = cos		π + isin		π = cos (2π −		) + isin (2π −		) = cos
	6		6		6		6		6

	π		√3		1
− isin		=		−		i
	6		2		2

Mógłby mi ktoś wytłumaczyć skąd tutaj cosinus sinus, skąd brac te wartości. I jak sie zabrac wogole do liczenia tego np. x² −i = 0, mialem to 4 semestry temu i kompletnie zapomnialem jak sie to robi. z góry dziękuje

Daniel: x² − i = 0

	π		π
x2 = i = cos		+ isin
	2		2

n = 2

	π		π		√2		√2
x0 = cos		+ isin		=		+		i
	4		4		2		2

	5		5		π		π		√2
x1 = cos		π + isin		π = cos (π+		) + isin (π+		) = −		−
	4		4		4		4		2

	√2
		i
	2

moze ktos sprawdzic czy dobrze, ewentualnie poprawic?

Adamm: x³+i³=0 x₀=−i, x₁=x₀*(1/2+i√3/2), x₂=x₀*(1/2−i√3/2)

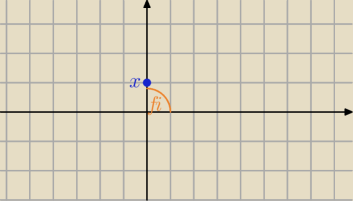Mila: x² − i = 0 x²=i x=√i |i|=1

	π
φ=
	2

	π   +2kπ 2		π   +2kπ 2
xk=|i|*(cos		+ i sin		)
	2		2

gdzie k∊{0,1}

	π		π		√2		√2
x0=1*(cos		+i sin		)=		+		*i
	4		4		2		2

	π   +2π 2		π   +2π 2
x1=(cos		+ i sin		) =
	2		2

	5π		5π		√2		√2
=cos		+i sin		=−		−		*i
	4		4		2		2

Daniel: czyli sa 2 opcje tylko

	π
φ =
	2

w przypadku kiedy i = 1 i

	3π
φ =
	2

w przypadku kiedy i = −1?

Daniel: w sesie modul z i

Mila:

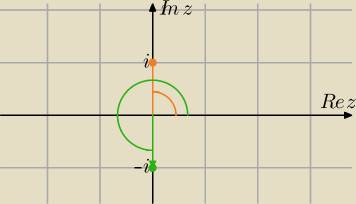
	π
z=i to φ=		, z=i to punkt(0,1)
	2

	3π
z=−i to φ=		, z=−i to punkt (0−1)
	2

Daniel: ok dzieki wielkie, w koncu sobie przypomnialem.

Mila: