Dany jest: Gracz32: Dany jest graniastosłup prawidłowy trójkatny o dolnej podstawie ABC i górnej A' B' C'. Przekątna ściany bocznej tworzy z krawędzią podstawy kąt 60 stopni. Pole ściany bocznej graniastoslupa jest równe 2pierw z 3. Oblicz pole trójkąta ABC'. To zadanie z matury próbnej z operon, ale proszę o własne rozwiązanie, a nie to że strony wydawnictwa.

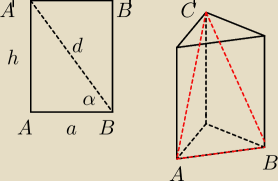
kochanus_niepospolitus: α = 60^o

	h
PABB'A' = 2√3 = a*h = a2*		= a2*tgα = a2√3 −> a = √2 ; h = √6
	a

d = √2+6 = √8 = 2√2 znając już długości boków tego graniastosłupa oraz przekątną ściany bocznej możemy obliczyć pole trójkąta ABC' Należy zauważyć, że jest to trójkąt równoramienny o ramionach d i podstawie a. Wyznaczamy wysokość tego trójkąta (tw. Pitagorasa):

	√30
H = √d2 − (a2/4) = √ 8 − 1/2 = √15/2 =
	2

	a*H		2√15		√15
PΔ =		=		=
	2		4		2

Gracz32: Wielkie dzięki. Czyli w odpowiedziach operonu raczej jest błąd, bo mi na maturze wyszło tak samo

mądra sowa: Operon ma dobrą odpowiedź, tu jest niedobre rozwiązanie

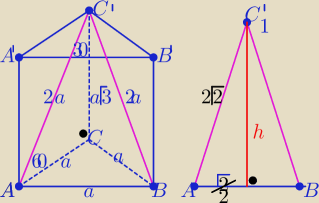
Eta: Bez f. trygonometrycznych .... z trójkąta "ekierki" P(ACA^'C^')=a²√3=2√3 ⇒ a²=2 ⇒ a=√2

	√15
h=√8−(1/2)=
	√2

	1		√15		√15
P(ABC')=		*√2*		=		[ j2]
	2		√2		2

kochanus_niepospolitus: mądra sowa −−− to gdzie jest błąd w obliczeniach

Eta: @mądra sowa Gdzie widzisz błąd? ..................

Eta: Myślę,że nie widzi w "Operonie"

Mateusz: W rozwiązaniu kochanus_niepospolitus PABB'A' =2√3=ah=a²*h/a=atgα czyli a=2 W rozwiazaniu Eta P(ACA'C')=1/2a²√3=2√3 ⇒ a²=4 ⇒ a=2 Operon podał dobrą odpowiedź

kochanus_niepospolitus:

	h		h
nie −−−> a*h = a2 *		= a2 * tg α (ponieważ tgα =		)
	a		a

kochanus_niepospolitus: niby dlaczego według Ciebie Mateusz −−− P(ACC'A') = P(ACC') Skoro P(ACC'A') = 2*P(ACC')

Eta: Ściana boczna jest prostokątem Pole prostokąta o wymiarach a i a√3 P=a²√3 a²√3=2√3 ⇒ a²=2 ⇒ a=√2 I tyle w tym temacie

Gracz32: @Mateusz P(ACA'C')=1/2a2√3=2√3 W tym równaniu użyłeś wzoru na pole trójkąta, a podane masz pole prostokąta mistrzu

Eta: