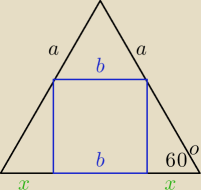
 widzę odpowiedź Jerzego ale tak długo rysowałam w tym edytorze, że jednak wysyłam!
a − dł.boku trójkąta
b − dł.boku kwadratu
a = b + 2x
widzę odpowiedź Jerzego ale tak długo rysowałam w tym edytorze, że jednak wysyłam!
a − dł.boku trójkąta
b − dł.boku kwadratu
a = b + 2x
| b | |
= tg 60o = √3 | |
| x |
| b | ||
x = | ||
| √3 |
| b | 2 | (√3+2) | ||||
a = b + 2* | = b(1+ | ) = b* | ||||
| √3 | √3 | √3 |
| a*√3 | ||
b = | ||
| (√3+2) |
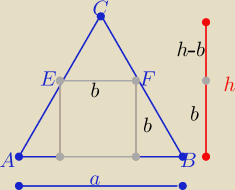 Z podobieństwa trójkątów ABC i EFC
Z podobieństwa trójkątów ABC i EFC
| b | h−b | b | b | a√3 | |||||
= | ⇒ | =1− | i h= | ||||||
| a | h | a | h | 2 |
| b | 2b | |||
+ | =1 /* a√3 | |||
| a | a√3 |
| a√3 | ||
b√3+2b=a√3 ⇒ b(√3+2)=a√3 ⇒ b= | = a(2√3−3) | |
| √3+2 |
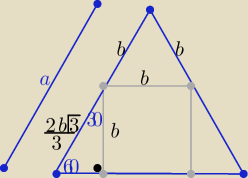 To jest najprostszy sposób ( na poziomie gimnazjum ( bez trygonometrii)
To jest najprostszy sposób ( na poziomie gimnazjum ( bez trygonometrii)
| 2b√3 | ||
b+ | =a ⇒ 3b+2b√3=3a⇒ b(2√3+3)=3a /*(2√3−3)⇒ b=a(2√3−3) | |
| 3 |