Planimetria Maciek: W trójkącie ABC dane są długości boków: AB=8 cm, AC=10 cm, BC=12 cm. Z punktu O, który jest środkiem boku BC, zakreślono okrąg o promieniu OB przecinający bok AB w punkcie D i bok AC w punkcie E. Oblicz długości boków DB i EC.

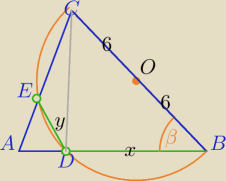
Mila: Podpowiedź: 1) oblicz cos β z tw. cosinusów w ΔABC 2) ΔCDB −Δprostokątny − 3) oblicz x korzystając z wartości cosβ dalej próbuj sam

Eta: 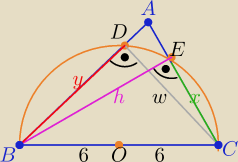2 sposób

	12+10+8
pole ABC ze wzoru Herona p=		= 15
	2

P(ABC) =√p(p−12)(p−10)(p−8)= ............ =15√7

	1
P(ABC)=		h*10 ⇒ h=....
	2

	1
P(ABC)=		w*8 ⇒ w=...
	2

i dwa razy z tw. Pitagorasa w ΔDBC i w ΔEBC y=√12²−w²=... x=√12²−h²=....

Mila: Do wyboru , do koloru

Eta: A zainteresowania ...... brak

Maciek: Dzięki za pomoc, już mi wyszło. Tak z ciekawości: jak zrobić to zadanie mając materiał tylko z gimnazjum? Było ono kilkanaście lat temu w konkursie dla gimnazjów w województwie kujawsko−pomorskim.

Mila: W sposobie Ety masz wiadomości z GM.

Czarek: Wzór Herona w gimnazjum? Cyba później wprowadzali...