Granica funkcji Maciek: Oblicz granicę funkcji, jeśli istnieje:

	cos2x − sin2x
limx → π/2
	|2x − π|

Wynik z książki się nie zgadza. Podszedłem do tego tak:

	1 − 2 sin2x
limx → π/2
	|2x − π|

	cos 2x
limx → π/2		⇒ (x = π/2 − u; u → 0)
	|2x − π|

	cos 2(π/2 − u)
limu → 0
	|2(π/2 − u) − π|

	sin 2u)
limu → 0
	|π − 2u − π|

	sin 2u)
limu → 0
	|−2u|

	sin 2u)		sin 2u)
− limu → 0−		= limu → 0−		= 1
	−2u		2u

	sin 2u)		sin 2u)
limu → 0+		= − limu → 0−		= −1
	−2u		2u

Z czego wynika, że granica nie istnieje. Odpowiedzi podają jednak, że istnieje granica niewłaściwa w −∞. Proszę o pomoc.

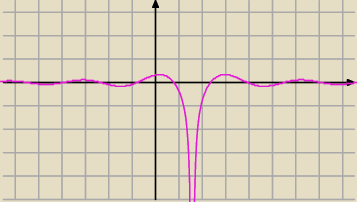Mila: cos²x−sin²x=cos(2x)

	cos(2x)		π
f(x)=		dla x>
	2x−π		2

	cos(2x)		π
f(x)=		dla x<
	−2x+π		2

	cos(2x)		−1
lim x→π2+		=[		]=−∞
	2x−π		0+

	cos(2x)		−1
lim x→π2−		=[		]=−∞
	−2x+π		0+

Maciek: Dziękuję bardzo. Dobrego dnia życzę.

Mila: Oj, nie jest dobry, duża awaria i brak gazu.

Maciek: Miejmy nadzieję, że jutrzejszy będzie lepszy.