proszę o rozwiązanie
Anna: rozwiąż równanie Ix2 −4I + Ix2 − 5I =1
czy takie równanie należy rozwiązywać po przedziałach
20 lis 21:30
Janek191:
Tak

20 lis 21:31
Janek191:
Tak

20 lis 21:31
Adamm: możesz sobie podstawić t=x2
|t−4|+|t−5|=1
t∊[4;5]
4≤x2≤5
itd.
20 lis 21:32
yht:
można
albo (lepiej) skorzystaj z tego że x2−5 = x2−4−1
i podstawienie x2−4 = t
|t| + |t−1| = 1
widać że równanie jest spełnione gdy t∊<0, 1>
podstaw sobie
t=0
t=0,1
t=0,2
t=0,3
t=0,4
t=0,5
t=0,6
t=0,7
t=0,8
t=0,9
t=1
zatem
x2−4 ∊ <0,1>
x2−4≥0 i x2−4≤1
(x−2)(x+2)≥0 i (x−√5)(x+√5)≤0
(x∊(−∞,−2>u<2,+∞) i (x∊<−√5,√5>)
i − część wspólna
Odp. x∊<−√5,−2> u <2,√5>
20 lis 21:34
Eta:
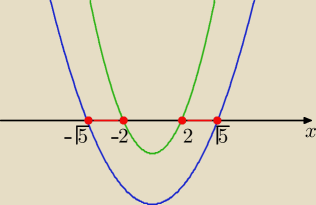
20 lis 21:40
Anna: dziękuję ja zrobiłam po przedziałach ale to długie liczenie
krótszy sposób jest tak jak zrobił yht 20 lis 21:34
21 lis 07:35


