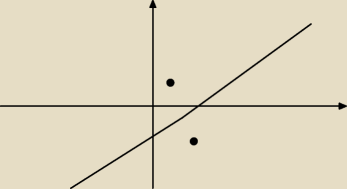
2 pytania z płaszczyzn zespolonych Kamil: 2 pytania z płaszczyzn zespolonych. 1 pytanie(rysunek) A={z∊ℂ: |z−3−2i|<|z−2+i|} wiem jak to się rysuje tylko którą część zaznaczyć? pod linią czy nad? i dlaczego? jak łatwo można to w głowie poukładać aby w przyszłości wiedzieć? 2 pytanie jak narysować B={z∊ℂ: Im(iz)>−6 ?

Maciek: w 1 masz kołka

Kamil: mylisz się, napewno jest dobrze narysowane, tylko jeszcze trzeba "zakreskować" którąś z półpłaszczyzn

Kamil: pomógłby ktoś?

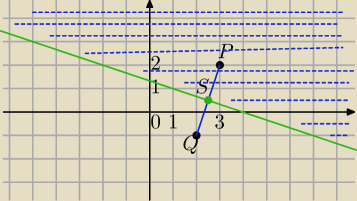
Mila: P=(3,2), Q=(2,−1)

	1		4
symetralna PQ: y=−		x+
	3		3

	1		4
y=−		x+
	3		3

A={z∊ℂ: |z−3−2i|<|z−2+i|} sprawdzam dla jednego punktu z półpłaszczyzny z=(0,0) |−3−2i|<? |−2+i| √9+4<? √4+1 fałsz zatem punkty nad symetralną spełniają podany warunek

Kamil: hmm a można tak postrzegać że zakreskowana będzie ta półpłaszczyzna na której leży punkt na który wskazuje dziób znaku nierówności? (mam nadzieję że wiesz o co chodzi) czyli tutaj A={z∊ℂ: |z−3−2i|<|z−2+i|} znak nierówności jest zwrócony dziobem do |z−3−2i| co reprezentuje P(3,2) więc kreskuję półpłaszczyznę na której leży punkt p.

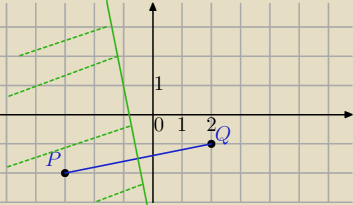
Mila: Nie : ja zapominam takie zasady. Ja sprawdzam, albo rozwiązuje podstawiając : z=x+iy B={z∊ℂ: |z+3+2i|<|z−2+i|} punkty leżą pod symetralną y=−5x−4

Mila: Może JC pokaże uproszczony sposób wyboru półpłaszczyzny.

Kamil: dzięki, a jak zrobić zad 2 z pierwszego postu?

Mila: B={z∊ℂ: Im(iz)>−6} z=x+iy, x,y∊R i*z=xi−y im(iz)=x x>−6 Na prawo od prostej x=−6 ( bez prostej)

Kamil: wielkie dzięki