Proszę o pomoc, muszę zrobić to na jutro, a pustka w głowie ;( Milena: Wykaż, że jeśli w dowolnym czworokącie ABCD dwusieczne kątów wewnętrznych wyznaczają czworokąt, to mozna na nim opisać okrąg.

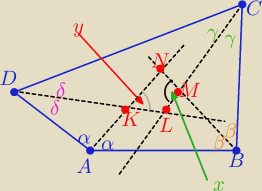
Eta: 1/ w czworokącie ABCD : 2α+2β+2γ+2δ=360^o ⇒ α+β+γ+δ=180^o 2/ |∡x|=|∡BMC|= 180^o−(β+γ) |∡y|=|∡AKD|= 180⁻(α+δ) to |∡x|+|∡y|= 360⁻(α+β+γ+δ) = 360^o−180^o= 180^o zatem na czworokącie KLMN da się opisać okrąg ( bo suma miar katów przeciwległych x+y=180^o)

Milena: Dziękuję

Eta: Na zdrowie ........

Eta: To teraz sama wykaż czy taka zależność zachodzi też dla dwusiecznych kątów zewnętrznych czworokąta ABCD

Eta: