Bardzo proszę o pomoc :) Krzysio: Obwód trapezu równoramiennego jest równy 30 cm, a odcinek łączący środki tych przekątnych trapezu ma długość 1,5 cm. Wiedząc, że w ten trapez można wpisać okrąg oblicz: a) długości podstaw trapezu b) długość średnicy okręgu wpisanego w ten trapez c) długość odcinka łączącego punkty styczności ramion z tym okręgiem.

Eta: Jak widzę trapez to ... ......... i rysuję

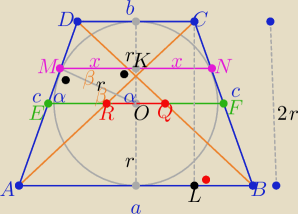
Eta: a,b −− długości podstaw trapezu c−− dł. ramienia trapezu a) z warunku wpisania okręgu w trapez : a+b=2c ⇒ Obwód : 2a+2b=30 ⇒ a+b=15

	a−b
|RQ|=|BL|=		= 1,5 ⇒ a−b=3
	2

−−−−−−−−−− 2a=18 to a=9 i b=6 to c=7,5 b) z tw. Pitagorasa w ΔCBL : 4r²= 7,5²−1,5² ⇒ 2r=3√6 to r=1,5√6

	a+b
c) |EF|=		to|EO|= 0,5|EF|= 3,75
	2

i z podobieństwa trójkątów EOM i MKO z cechy(kkk)

	x		r		r2
		=		⇒ x=		=............. = 3,6
	r		|EO|		3,75

to szukana odległość między punktami styczności 2x=|MN|= 7,2

Krzysio: Jejkuuu 😍 Dziękuję bardzo

Eta: Na zdrowie łap...........