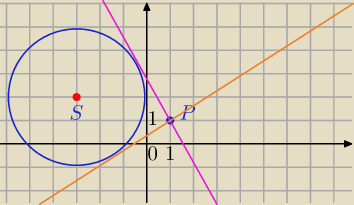
rownanie okregu styczne rzut na prostą: Znajdz równania stycznych do okręgu o równaniu (x+3)² + (y−2)² = 9, przechodzących przez punkt (1,1)

rzut na prostą: up

5-latek: Za chwile pomoge

5-latek: samemu rysunek bo prosto srodek okregu ma wspoirzedne S=(−3,2) i promien r=3 Pek prostych przechodzacych przez punkt A=(1,1) ma rownaanie y−1= m(x−1) −mx+y+m−1=0 mx−y+1−m=0 (postac ogolna Teraz wzor na odlegosc punktu od prostej

	|mx0−y0+1−m|
d=
	√m2+1

Wiemy ze d=3 (bo odleglosc srodka okregu od prostej skoro ma byc styczna jesst rowna promieniowi i za x₀ i y₀ wstawaimy wspolrzedne srodka okregu

	|−3m −2+1−m|
3=
	√m2+1

inaczej sobie zapiszse

|−4m−1
	=3
√m2+1

Wylicz z tego m i wstaw do rownania mx−y+1−m=0 i napisz te rownania stycznych

Mila: (x+3)² + (y−2)² = 9 S=(−3,2) r=3 P=(1,1) 1) styczna : s: y=ax+b i P∊s⇔ 1=a+b ⇔b=1−a y=ax+1−a⇔ax−y+1−a=0 2) odległość S od stycznej jest równa r=3

	|a*(−3)−1*2+1−a|
d(S, s)=		=3⇔
	√a2+12

|−4a−1|=3*√a²+1⇔|4a+1|=3*√a²+1 /² 16a²+8a+1=9a²+9

	−4−6√2		−4+6√2
a=		lub a=
	7		7

napisz równania stycznych......

5-latek: Dobry wieczor Milu

Mila: Witam