Funkcje odwrotne
max: Wyznaczyć dziedzinę i funkcję odwrotną:
| | x−3 | |
a) f(x) = 3arcsin ( |
| ) |
| | x+1 | |
b) f(x) =
√log15 (2x−5)
ad a)
Df:
x+1 ≠ 0
x ≠ −1
−3x − 3 ≤ x−3 ≤ 3x + 3
−4x ≤ 3x + 3
−7x ≤ 3
| y | | x−3 | |
| = arcsin |
| / *sin |
| 3 | | x+1 | |
| | y | | x−3 | |
sin |
| = |
| /*(x+1) |
| | 3 | | x+1 | |
| | x | |
f−1 (x) = sin |
| (x+1) + 3 |
| | 3 | |
ad b)
f(x) =
√log15 (2x−5)
Df:
2x − 5 > 0
2x > 5
log
15(2x−5) ≥ 0
log
15(2x−5) ≥ log
151
2x − 5 ≥ 1
2x − 5 ≥ 0
2x ≥ 4
x ≥ 2
y =
√log15 (2x−5) / ()
2
y
2 = log
15(2x−5)
i nie wiem co dalej do odwrotnej w b)
Proszę o sprawdzenie czy jest dobrze dla a) i o pomoc przy b)
19 lis 19:53
max: Bardzo proszę o pomoc

19 lis 20:07
max: bump
19 lis 20:30
piotr: w a) dziedziną jest x≥1, bma być −1 <= (x − 3)/(x + 1) <= 1
19 lis 20:43
max: Czyli
−1 <= (x − 3)/(x + 1) <= 1 / *x+1
−x−1 ≤ 3 − x ≤ x+1
−4 ≤ x+1
−5 ≤ x
x ≤ −5

19 lis 20:50
piotr:
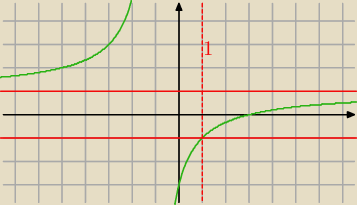
19 lis 20:55
piotr: widzę, że masz problemy z prostymi nierównościami wymiernymi
19 lis 20:56
max: piotr, no dobrze, rozumiem, ale czemu x ≥ 1, przecież w mianowniku nie może być zero
19 lis 21:02
piotr: przecież jak podstawisz cokolwiek większe równe 1 to nie będzie 0
a funkcja odwrotna wygląda tak:
19 lis 21:14
piotr: masz błąd w miejscu poniżej:
(x+1)sin(y/3) = x−3
19 lis 21:17
max: A czemu tam jest źle? Nie mogę przenieść 3?
19 lis 21:23
piotr: musisz wyznaczyć z tego x:
x sin(y/3)+ sin(y/3) = x−3
x sin(y/3) − x = −3 − sin(y/3)
x (sin(y/3) − 1) = −3 − sin(y/3)
| | −3 − sin(y/3) | |
x = |
| |
| | sin(y/3) − 1 | |
19 lis 21:30
max: Ooo, piotr, dzięki, czaję już.
A tej dziedziny nie można czasem rozbić tak?:
−x−1 ≤ x−3
−2x ≤ −2
x ≥ 1
i
x−3 ≤ x + 1
−3 ≤ 1
I wtedy to drugie odrzucamy?
19 lis 22:04
piotr: nie wolno wymnażać przez x+1, bo nie wiadomo jaki znak ma to wyrażenie, a to może zmienić lub
nie znak nierówności
trzeba przenieść 1 i wziąć wspólny mianownik
będzie:
a z drugiego:
20 lis 22:20


