| 1 | π | 5π | ||||
wyznaczyc zbior wartosci funkcji f(x)= | gdzie x∊< | ; | > | |||
| sinx | 4 | 6 |
 (pazdro, 3klasa analiza matematyczna temat ciaglosc fukcji )
(pazdro, 3klasa analiza matematyczna temat ciaglosc fukcji )
 x∊[π/4; 5π/6]
więc
sinx>0
t=sinx
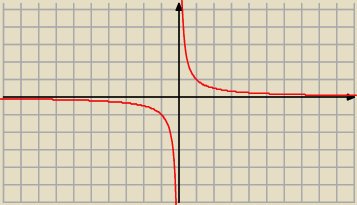
rysujemy sobie hiperbolę
g(t)=1/t
patrzymy, no tak!
dla dodatnich jest malejąca
dla x∊[π/4; π/2] sinus rośnie
więc
f(x) maleje (bo złożenie funkcji rosnącej i malejącej jest funkcją malejącą)
dla x∊[π/2; 5π/6] sinus maleje
czyli f(x) rośnie
dalej mam nadzieję że student sobie poradzi...
x∊[π/4; 5π/6]
więc
sinx>0
t=sinx
rysujemy sobie hiperbolę
g(t)=1/t
patrzymy, no tak!
dla dodatnich jest malejąca
dla x∊[π/4; π/2] sinus rośnie
więc
f(x) maleje (bo złożenie funkcji rosnącej i malejącej jest funkcją malejącą)
dla x∊[π/2; 5π/6] sinus maleje
czyli f(x) rośnie
dalej mam nadzieję że student sobie poradzi...
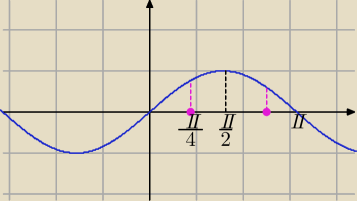 g(x)=sin (x)
g(x)=sin (x)
| π | ||
dla x= | wartość największa g(x) w podanym przedziale, | |
| 2 |
| π | ||
sin | =1 | |
| 2 |
| 5π | ||
dla x= | wartość najmniejsza g(x) w podanym przedziale | |
| 6 |
| π | √2 | 5π | 1 | |||||
sin | = | >sin | = | |||||
| 4 | 2 | 6 | 2 |
| π | 1 | |||
f( | )= | =1 | ||
| 2 | 1 |
| 5π | 1 | |||
f( | )= | =2 | ||
| 6 | 0.5 |
| π | 5π | |||
sinx≠0 dla x∊< | , | > | ||
| 4 | 6 |