prostokąt Marcin: 1) Z wierzchołka B prostokąta ABCD poprowadzono prostą prostopadłą do przekątnej BC Odległości punktów A i C od tej prostej są odpowiednio równe 36 i 64 Oblicz długości boków tego prostokąta 2) Na boku AB równoległoboku ABCD obrano punkt E tak,że |AE| : |AB|=2:3 Odcinki DE i AC przecinają się w punkcie F Punkt S jest punktem przecięcia przekątnych równoległoboku Wykaż,ze pole trójkąta FSD stanowi 5% pola równoległoboku Bardzo proszę o pomoc w rozwiązaniu tych zadań wraz z rysunkiem

5-latek: Marcin rysunek to bez jaj Nie potrafisz narysowac prostokata czy rownolegloboku ? To ma byc szkic tylko nie taki niedbaly

Eta:

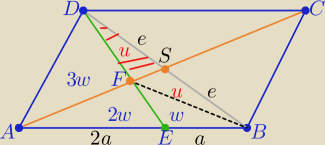
Eta: Zad.2 P−− pole równoległoboku u−− pole ΔFSD Z treści zadania : |AE|=2a , |EB|=a i z oznaczeń na rysunku ( uzasadnij je 2(2u+w)=5w ⇒ 4u=3w

	1		1		1
P(ASD)=		P(ABCD) ⇒		P=3w+u=5u ⇒ u=		P = 5%P
	4		4		20

c.n.w

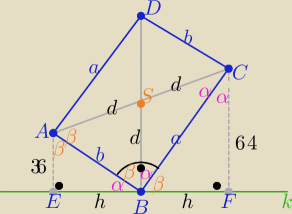Eta: Zad2/ W treści masz błąd ... pewnie ma być ... prostopadła do przekątnej BD Podaję jeden ze sposobów rozwiązania (może ktoś poda jeszcze inny sposób a, b −− dł. boków prostokąta ,które mamy obliczyć BS −− jest środkową ΔABC

	36+64
i jednocześnie środkową trapezu prostokątnego AEFC ⇒|BS|=		=50
	2

to |AC|=100 α+β= 90^o Zauważ trzy trójkąty podobne : AEB i BFC i ABC z cechy (kkk)

	64		a
to:		=		⇒ a=80
	a		100

	36		b
		=		⇒ b= 60
	b		100

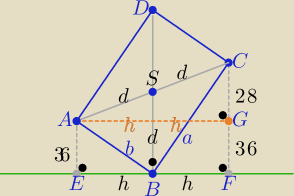Eta: 2 sposób d=50 to 2d=100 ( podobnie jak w pierwszym sposobie) teraz dorysuj odcinek AG ∥ EF ⇒ |AG|=|EF|=2h i |GC|=64−36= 28 z tw. Pitagorasa wΔCAG wyznacz długość h.......... h=48 i dwa razy z tw. Pitagorasa w ΔAEB i w ΔBFC wyznaczysz szukane długości b i a

Eta:

Mila: Witaj Eto, treść (1)? Co z zadankiem dla Filipka?

Eta: Hej Mila Filip obecnie choruje na ostrą grypę więc nie chcę go zamęczać zadaniami

Mila: To poczekamy. Zdrówka życzę