granica
analizamatematyczna1: Oblicz granice ciągu w nieskończoności
| | 1+2+...+n | |
an = |
| * cos n! |
| | n | |
18 lis 23:26
Janek191:
| | 0,5n*(n +1) | |
an = |
| *cos n ! = 0,5*( n +1)*cos n ! |
| | n | |
19 lis 00:12
5-latek: czy granica tego ciagu bedzie (∞) ?
lim n→∞0,5(n+1)=∞
ciag cosn! jest oragniczony wiec ich iloczym zmierza do ∞
19 lis 10:39
5-latek:
19 lis 10:50
iteRacj@:
witaj

zauważ, że cos n! będzie przyjmowac wartości zarówno dodatnie jak i ujemne
19 lis 10:57
g: Nie ma granicy. cos(n!) może być równie dobrze dodatni i ujemny.
Nawet gdyby było |cos(n!)| to też granicą nie było by ∞. Nie dało by się spełnić warunku
∀M ∃N (n≥N: an≥M)
19 lis 10:57
5-latek: Witam
iteRacj@ i
g 
Dobrze .
19 lis 11:02
5-latek: Zapytalem z tego wzgledu ze ma taki przyklad
Tutaj korzystam ze mam ciag zbiezny do zera i ciag ograniczony
wiec granica to 0
Z tego co napisaliscie to sin(n+
√n tez moze przyjmowac wartosci dodatnie i ujemne .
Wiec jaka tutaj jest miedzy nimi roznica ?
19 lis 11:11
5-latek:
19 lis 11:46
iteRacj@:
jeśli nikt nie odpowie wcześniej , to napiszę to za pół godziny
19 lis 11:48
5-latek: Dobrze bede czekal .
19 lis 11:50
iteRacj@:
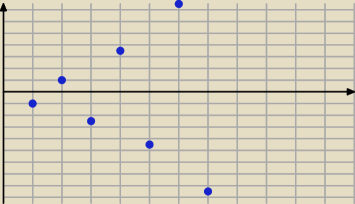
wytłumaczę na przykładzie innych ciągów, będzie mi łatwiej
masz ciąg a
n = 3n
2*(−1)
n, ciąg a
n przyjmuje wartości dodatnie i ujemne
wyraźnie widać dwa podciągi: jeden rozbieżny o wyrazach dodatnich i drugi też rozbieżny o
wyrazach ujemnych,
wyrazy "się rozbiegają "
| | 1 | |
w ciągu bn = |
| *(−1)n (nastepny rysunek) wyrazy też będą przyjmować wartości i |
| | 3n2 | |
dodatnie i ujemne, ale oba podciągi będą zbieżne,
wyrazy "zbiegają " do tej samej wartości
19 lis 12:58
iteRacj@:
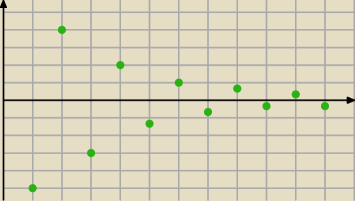
19 lis 13:00
5-latek: Bardzo dziekuje za wyjasnienie

19 lis 13:03
 zauważ, że cos n! będzie przyjmowac wartości zarówno dodatnie jak i ujemne
zauważ, że cos n! będzie przyjmowac wartości zarówno dodatnie jak i ujemne
 Dobrze .
Dobrze .
 wytłumaczę na przykładzie innych ciągów, będzie mi łatwiej
masz ciąg an = 3n2*(−1)n, ciąg an przyjmuje wartości dodatnie i ujemne
wyraźnie widać dwa podciągi: jeden rozbieżny o wyrazach dodatnich i drugi też rozbieżny o
wyrazach ujemnych,
wyrazy "się rozbiegają "
wytłumaczę na przykładzie innych ciągów, będzie mi łatwiej
masz ciąg an = 3n2*(−1)n, ciąg an przyjmuje wartości dodatnie i ujemne
wyraźnie widać dwa podciągi: jeden rozbieżny o wyrazach dodatnich i drugi też rozbieżny o
wyrazach ujemnych,
wyrazy "się rozbiegają "

