parametry... kat: Funkcja f określona jest wzorem f(x) = −x² + bx + c. Zbiorem rozwiązań nierówności f(x) < 0 jest zbiór (−∞;+∞). Sprawdź obliczeniowo czy prawdziwa jest nierówność: c >¹₄ * b².

kat: Z analizy zadania wiem, że cały wykres funkcji leży pod osią x. Co dalej z tym zrobić?

Jerzy: Skoro taka analiza, to musi być: Δ < 0 b² − 4*(−1)*c < 0 ⇔ ..... i dokończ.

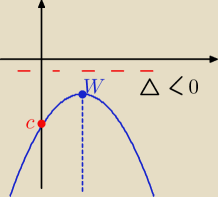
Eta: Cały wykres pod osią to oznacza ,że c<0 i Δ<0

	1
Δ= b2−4(−1)*(−c)<0⇒ b2−4c<0 ⇒ 4c>b2 ⇒ c>		b2
	4

Jerzy: Daremne żale, próżny trud... Witaj

kat: Skąd wziął się ten minus przy współczynniku c? W założeniach przyjęliśmy, że c jest mniejsze od 0. Ok, samo c. A dodając do tego minus powstanie liczba dodatnia. Nie rozumiem.

kat: Chodzi mi o rozwiązanie Eta. Odpowiedź rzeczywiście się zgadza, ale skąd to c z dodatkowym minusem nie wiem skąd przy liczeniu delty...

kat:

Jerzy: f(0) = c < 0

5-latek: Gdzie teraz znajdziesz dentyste jak cie bola zęby ? Poczekaj na Panią Ete moze sie pojawi na forum Nie lubi jak ktos sie jej wtraca w zadanie

kat: Tak, c < 0, ale przecież skoro zakładamy, że c jest mniejsze od 0 to automatycznie jest to liczba ujemna i nie jest potrzebny dodatkowy minus, aby to pokazać.

Eta: Już wyjaśniam Chciałam Ci pokazać abyś wyraźniej widział/ła że jeżeli c<0 to Δ= b² −4 *(−1)c = b²−4ac

Jerzy: Masz 100% racji,nierówność wyjściowa jest fałszywa.

Eta: ?

kat: Ale dodając minus, automatycznie zmienia się całe rozwiązanie. Δ = b² − 4ac i Δ < 0 więc: b² − 4ac < 0 b² < 4(−1)c b² < −4c c > − 1/4 * b² W Twojej odpowiedzi nie ma "−" na początku i stąd zastanawiam się dlaczego tak jest. Odpowiedź bez minusa jest rzeczywiście prawdziwa, ale dlaczego?

kat: Przecież skoro c jest liczbą ujemną, to −c jest dodatnie.

kat: ?

kat: Ktoś ma jakiś pomysł? Proszę o pomoc...

'Leszek: @kat, p.Eta wylozyla Ci " kawe na lawe " dokladniej juz sie nie da , popatrz do podrecznika , tam sa wyrysowane wszystkie przypadki z funkcja kwadratowa !

kat: Nadal nie mam odpowiedzi dlaczego pojawił się minus przy c. Skoro c jest liczbą ujemną to wstawienie minusa przed c sprawia, że jest to liczba dodatnia! Tylko i wyłącznie to mnie zastanawia. Nie chcę gotowego rozwiązania. Nie chce żeby ktoś odrabiał za mnie pracę domową. Chcę jedynie prosić o wyjaśnienie skąd ten minus się tam wziął.. Czy naprawdę to powód żeby obrażać?

kat:

iteRacj@: @kat nikt się nie obraża, po prostu nie ma jak inaczej tego wyjasnić niż opisowo lub rysunkiem oba te sposoby juz zostały użyte napisałaś, że funkcja przyjmuje jedynie wartości ujemne dla x=0 mamy f(0) = −0² + b*0 + c = c więc c też jest ujemne, to widać na rysunku Ety

	1
jak nierówność c >		* b2 może być prawdziwa skoro c jest ujemne?
	4

	1
l. ujemna >		* b2 ?
	4

kat: Tak, tylko że Eta nie mam pojęcia z jakiego powodu dodała minus w swoich obliczeniach przed c i dlatego wyszła jej taka nierówność. Ja starałam się obliczyć według tego, że c jest ujemne − tzn. nie dodawać tam kolejnego minusa, tylko po prostu wpisać c jako c, i tyle. Z moich obliczeń wyszło coś takiego: b² − 4ac < 0 b² < 4(−1)c b² < −4c c > − 1/4 * b² Rozwiązanie Ety jest takie samo, tylko prawa strona różni się u niej znakiem. Jasne, zgadzam się z Wami chociażby z tym, że liczba ujemna nie może być większa od tego wyrażenia po prawej... Ale gdzie w rozumowaniu popełniłam błąd, że mi wyrażenie po prawej wyszło z minusem, a Wam z plusem.

kat: Co więcej, najlepsze jest to, że zbiór, z którego korzystam w odpowiedziach ma zapisane, iż nierówność c > 1/4 b² jest prawdziwa, co zupełnie niszczy wszystkie nasze wspólne dotychczasowe ustalenia.

kat: Wiem, że ciężko jest wytłumaczyć o co chodzi pisząc, a jeszcze ciężej zapewne jest to zrozumieć, aczkolwiek nie wiem jak innymi słowami miałabym wyrazić o co mi chodzi...

iteRacj@: poddaję się, nie wiem, dlaczego w zbiorze jest taka odpowiedź rozumiem odpowiedź Jerzego, rozumiem odpowiedź Ety nie rozumiem odpowiedzi ze zbioru

kat: Mogę mieć jeszcze jedno pytanie w takim razie, czy myślisz, że to już przesada? Jeśli mogę, to odpowiedz; jeśli nie to po prostu zignoruj. Skoro napisałeś, że rozumiesz odpowiedź Ety, to mógłbyś mi wyjaśnić dlaczego w tej pierwszej odpowiedzi Ety (18 lis 17:45) pojawia się znak minus przed c? Ustaliliśmy, że c jest liczbą ujemną. Zgadzam się. Więc jeśli, dla przykładu, pod c skrywałoby się −4, to żeby napisać że jest to liczba ujemna to niepisalibyśmy −c, czyli −(−4)= +4, tylko po prostu c, pod którym kryłoby się −4, to o które nam chodzi. Eta napisała: Δ= b²−4(−1)*(−c)<0⇒ ... czyli już tutaj zaznacza, że c to nie c tylko −c. Dlaczego tak jest?

Jerzy: Mamy: a = −1 i Δ < 0

	b2
Δ = b2 − 4ac = b2 − 4*(−1)*c = b2 + 4c < 0 ⇔ 4c > −b2 ⇔ c < −		,
	4

czyli nierównoiść wyjśćiowa jest fałaszywa.

Jerzy: To,że c jest liczbą ujemną, nie mażadnego znaczenia w rozwiązaniu tego zadania. Mamy tylko dwa warunki: a = −1 i Δ < 0 ( znak c nas nie interesuje )

Jerzy:

	b2		b2
Jest prawdą,że: − c >		, czyli nie jest prawdą,że: c >
	4		4

iteRacj@: moim zdaniem − chodzi tu o pokazanie że tylko po zmianie postaci wyjściowej funkcji f(x) i to zmianie w ten sposób można otrzymać nierówność prawdziwą może odpowie Eta jeszcze trafi na ten wątek i odpowie

kat: O właśnie. Dokładnie o to mi chodziło. Cały czas zastanawiałam się, gdzie w rozwiązaniu Ety podział się ten minus.