Funkcja wymierna- Andrzej Kiełbasa
Tomek: | | |x2 − 1| | |
Funkcja f dana jest wzorem f(x)= |
| |
| | x3 −x | |
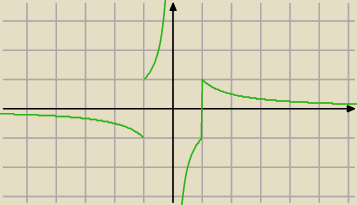
a)Naszkicuj wykres tej funkcji.
b) Dla jakich wartości parametru m równanie f(x) = m ma jedno rozwiązanie ?
Naprowadzimy mnie ktoś ?

18 lis 16:06
Adamm: x≠0
x
2−1>0
x
2−1<0
i tyle, rysujesz zwykłą hiperbolę
18 lis 16:12
===:
1. Zacznij od dziedziny
2. Załóż przedziały
3. Alleluja i do przodu

18 lis 16:12
===:
18 lis 16:15
'Leszek: Dziedzina : x3−x ≠ 0 ⇒ x = R− { −1,0,1}
a) dla x= (−∞ −1) ∪ (1,∞)
f(x) =1/x
b) dla x= (−1,0) ∪ (0,1)
f(x) = − 1/x
18 lis 16:15
Tomek: Dziękuję

Moglibyście jeszcze bardziej obrazowo objaśnić mi jak zrobić przykład b ?
18 lis 16:31
===:
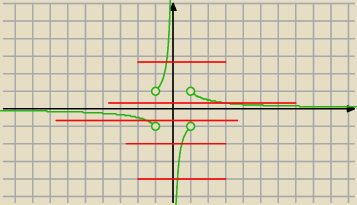
18 lis 16:38
Tomek: A jeśli miałbym zrobić to algebraicznie ?
18 lis 16:38
===:
Twoja funkcja jest różnowartościowa ... nie ma zatem nic do liczenia

... a liczenie do najłatwiejszych nie należałoby

18 lis 16:47
Tomek: Ok, dziękuję wszystkim za pomoc

18 lis 16:48
===:

18 lis 16:51



 Moglibyście jeszcze bardziej obrazowo objaśnić mi jak zrobić przykład b ?
Moglibyście jeszcze bardziej obrazowo objaśnić mi jak zrobić przykład b ?

 ... a liczenie do najłatwiejszych nie należałoby
... a liczenie do najłatwiejszych nie należałoby 

