trójkąt Marcin: W trójkącie ABC na bokach AC i BC obrano odpowiednio punkty D i E tak,że |DC|=3|AD| i |BE|=2|EC| Odcinki AE i BD przecinają się w punkcie M oraz prosta MC przecina bok AB w punkcie F a)oblicz pole trójkąta ABC wiedząc,że pole trójkąta AMD jest równe 12

	|MC|
b) wyznacz stosunek odcinków
	|MF|

Siedzę na tym zadaniem już ponad 4 godziny i nic nie wymyśliłem Bardzo Was proszę o pomoc

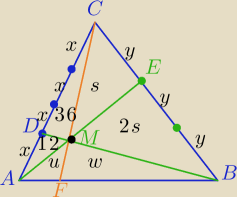Mila: P_ΔABC=P 1) P_ΔDMC=3*P_ΔADM=36

	1
PΔAEC=		P=12+36+s=48+s
	3

	3		3
PCDB=		P=36+s+2s⇔		P=36+3s /:3
	4		4

1
	P=12+s
4

1		1
	P−		P=48+s−12−s
3		4

1
	P=36
12

P=12*36=432 2)

Mila: 2)

	1		432
PΔADB=		P=		=108
	4		4

u+w=96

	1
PΔAEC=		P=144
	3

144=48+s s=96 3) z twierdzenia Cevy:

AF		2y		3x
	*		*		=1
FB		y		x

AF		1
	=
FB		6

4) w=6*u u+6u=96

	96
u=
	7

	6*96
w=
	7

	CM		PCMB		3s		3*96
5)		=		=		=		⇔
	MF		PBMF		w		6*96   7

CM		7
	=
MF		2

============== Posprawdzaj rachunki, albo zgodność z odpowiedzia.

Eta:

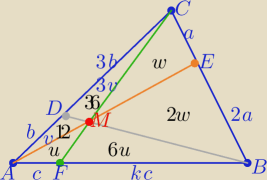
	kc		b		a
Z twierdzenia Cevy :		*		*		=1 ⇒ k=6
	c		3b		2a

3(12+7u)= 36+3w⇒ w=7u

	96		w
i 2(12+36+w)=2w+7u ⇒ 7u =96 to w=96 i u=		⇒		=7
	7		u

P(ABC)= 12+36+7u+3w= 48+4w= 432 [j²] =======

	|MC|		3w		w		7
b)		=		=		=
	MF|		6u		2u		2

=====

Eta: Hej Mila Wyniki zgodne Zainteresowany pewnie zmęczony ....4 godzinami

Mila: Tak, witam Jutro zobaczy.

Marcin: Bardzo Wam dziękuję

Mila: