Zadanie z próbnej matury
Natalia: W trójkącie prostokątnym kąty ostre mają miary α, β, przeciwprostokątna ma długość 13, a
sinα+ sinβ= 17:13 i sinα − sinβ= 7:13. Wynika z tego, że:
a) tgα= 5:12
b) tgα= 12:13
c) tgα= 10:13
d) tgα= 12:5
16 lis 11:43
iteRacj@: d) tgα= 12:5
16 lis 12:43
PW:
Po dodaniu stronami dostejemy
| | 12 | |
Teraz rysunek trójkąta, w którym przeciwprostokątna ma długość 13. Ponieważ sinα= |
| i |
| | 13 | |
przeciwprostokątna ma długość 13, widać że przyprostokątna ma długość 12. Drugą
przyprostokątną wyliczymy z tw. Pitagorasa.
Mając ją wyliczymy tgα.
16 lis 12:49
PW: No i wyszło na to, że tłumaczę w jaki sposób
iteracj@ to obliczyła. Tłumaczenie trwa
jednak znacznie dłużej niż obliczenie w pamięci.
16 lis 12:52
iteRacj@: PW troszkę inaczej liczyłam
ale najpierw sprawdziłam, że próbna dopiero za tydzień
Ty masz bardziej pedagogiczne podejście i Twoja odpowiedź jest o wiele lepsza
16 lis 13:14
Eta:
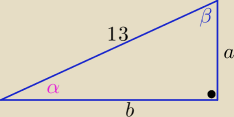
| | a | | b | |
sinα= |
| , sin β= |
| i c=13 |
| | c | | c | |
to
a+b=17
a−b= 7
+ −−−−−−−−
2a=24 ⇒ a=12 to b=5
odp: d)
16 lis 21:19
Mila:
Eta ?
16 lis 21:54
Eta:
Hej
Mila
Co?
16 lis 23:01
Ajtek:
Cześć Dziewczyny, fajne zadanko, pochylę się nad nim jutro. Chociaż przychodzi mi do głowy
paradoks Achillesa i żółwia.
16 lis 23:44
Mila:
Witaj
16 lis 23:44
Mila:
Super. Dziękuję
Eto.
16 lis 23:45
Eta:
Hej
Ajtek i łap............
16 lis 23:46
Ajtek:
Złapałem, ale czy nie robaczywe ;
16 lis 23:46
Eta:
Dla Ciebie ?............ same dobre
16 lis 23:49
Ajtek:
Na "przetwory"
16 lis 23:50
Mila:
Dobranoc
16 lis 23:50
Eta:
Dobranoc
Mila 
16 lis 23:51
Ajtek:
Spokojnej
Mila .
16 lis 23:51