z
qwerty: Ostrosłup ABCS ma w podstawie trójkąt równoboczny ABC o boku długości 6. Krawędź AS jest
wysokością ostrosłupa. Wiedząc, że objętość ostrosłupa wynosi 24√3 oblicz pole największej
ściany bocznej.
proszę o rysunek
15 lis 23:13
Eta:
P= 3√91
15 lis 23:19
qwerty: proszę o rysunek
15 lis 23:23
Eta:
.............................
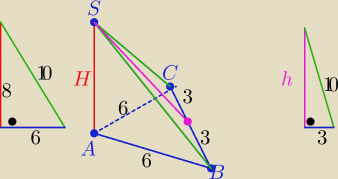
P(BCS)= 3*
h=..............
15 lis 23:26
qwerty: dzieki
15 lis 23:27
Eta:
15 lis 23:28
qwerty: skąd ten trójkąt prostokątny 8 6 10 nie widzę kątu prostego
15 lis 23:38
Eta:
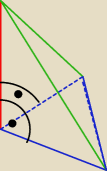
Postaw na stole dwie złączone ekierki .... to zobaczysz kąt prosty
15 lis 23:48
Eta:
| | 1 | 36√3 | |
V= |
|
| *H ⇒ 3√3H=24√3 ⇒ H=8 |
| | 3 | 4 | |
z trójkąta prostokątnego ABS z tw. Pitagorasa
|BS|=.......... =10
15 lis 23:52