Rownanie Gość1: Rozwiąz równanie 3x³−7x²+x −2=0

mat: met. Newtona

Mariusz: Można sprowadzić do równania kwadratowego bez zespolonych Gdyby metoda algebraiczna wymagała liczb zespolonych to chyba lepiej byłoby skorzystać z trygonometrii

	7
Podstawieniem y=x+		usunąć wyraz z x2
	9

Po zastosowaniu podstawienia y=u+v równanie pogrupować i zapisać w postaci układu równań Układ równań przekształcić tak aby przypominał wzory Vieta dla trójmianu kwadratowego

Olcia: Musisz obliczyć to z tabelki Hornera. Czyli jak postawisz za x=2 równanie będzie 0.

Mila: Olcia , w(2)=−4≠0 To równanie nie ma pierwiastków wymiernych. Czy dostałeś polecenie, aby rozwiązać to równanie, czy inne polecenie?

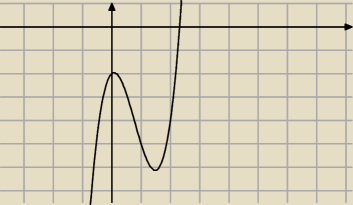PW: Olcia, ta złośliwa funkcja nie poddaje się takim łatwym sposobom. Źle liczysz f(2).

Kamil: Twierdzenie Darboux

Olcia: Sory, chyba jednak to nie będzie 2. Musisz poszukać innej liczby. Takiej jak postawisz, żeby wyszli 0. I potem tabelka Hornera

Mariusz: 3x³−7x²+x −2=0

	7		7		7
3(y+		)3−7(y+		)2+(y+		)−2=0
	9		9		9

	7		49		343		14		49		7
3(y3+		y2+		y+		)−7(y2+		y+		)+y+		−2=0
	3		27		729		9		81		9

	49		343		98		343		7
3y3+7y2+		y+		−7y2−		y−		+y+		−2=0
	9		243		9		81		9

	40		−686+7*27−486
3y3−		y+		=0
	9		243

	40		983
3y3−		y−		=0
	9		243

	40		983
y3−		y−		=0
	27		729

	40		983
y3−		y−		=0
	27		729

y=u+v

	40		983
(u+v)3−		(u+v)−		=0
	27		729

	40		983
u3+3u2v+3uv2+v3−		(u+v)−		=0
	27		729

	983		40
u3+v3−		+3(u+v)uv−		(u+v)=0
	729		27

	983		40
u3+v3−		+3(u+v)(uv−		)=0
	729		81

	983
u3+v3−		=0
	729

	40
uv−		=0
	81

	983
u3+v3=
	729

	40
uv=
	81

	983
u3+v3=
	729

	64000
u3v3=
	531441

	983		64000
t2−		t+
	729		531441

	983		966289		256000
(t−		)2−		+
	1458		2125764		2125764

	983		710289
(t−		)2−
	1458		2125764

	983−√710289		983+√710289
(t−		)(t−		)
	1458		1458

	3932−4√710289		3932+4√710289
(t−		)(t−		)
	5832		5832

	1
y=		(3√3932−4√710289+3√3932+4√710289)
	18

	7
x=y+
	9

	1
x=		(3√3932−4√710289+3√3932+4√710289+14)
	18