prosze o pomoc Dor: Dany jest trójkąt ABC, gdzie A(−1,−4), B(1,4), C(−3,5). Jaką długość ma najdłuższa z jego wysokości?

kochanus_niepospolitus: 1) sprawdzasz jaki bok jest najkrótszy 2) wyznaczasz wzór prostej zawierającej tenże bok 3) wyznaczasz wzór prostej PROSTOPADŁEJ do tamtej prostej i przechodzącej przez trzeci wierzchołek 4) wyznaczasz długość wysokości (odległość wierzchołka od punktu przecięcia się prostych) lub zamiast punktów 3 i 4 3*) stosujesz wzór na odległość puntu od prostej (wyznaczonej w punkcie (2) )

PW: Albo "poprzez pole". Liczyć pole S tego trójkąta (za pomocą wyznacznika lub wzoru Herona) i korzystając z wzoru

	1
S =		bk,hk k = 1, 2, 3
	2

liczyć wysokość h_k opuszczoną na bok o długości b_k. Widać to, o czym pisze kochanus₋niepospolitus − najdłuższa jest wysokość opuszczona na najkrótszy bok (bo iloczyn S jest stały).

Dor: Najkrótszy bok to AB

	25√17
Tylko teraz jakby wychodzi mi coś takiego:		i to jest raczej źle..
	17

PW: teraz jakby wychodzi mi coś takiego − o czym Ty mówisz? W pracy egzaminacyjnej też tak napiszesz? Policzyłeś pole S tego trójkąta? Pokaż jak.

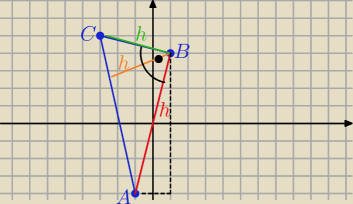
Eta: 1/ sprawdzamy jaki to trójkąt : |AB|²=68, |AC|²=85 , |BC|²= 17 to 68+17=85 −−− trójkąt prostokątny zatem najdłuższa wysokość to h=|AB|= .......... √68=2√17

PW: Jednak geometria analityczna kocha rysunki.

Dor: Na pracy egzaminacyjnej to się chyba rozpłaczę..

Eta:

PW: Dor, nie dołuj się. Będzie dobrze, ale pracuj (z nami też). Warto byś spróbował rozwiązać to zadanie metodą kochanusa.

Eta: Na egzaminach nie ma na to czasu