suriekcja
Kamil: Witam, jak udowodnić że funkcja jest suriekcją, czyli dla każdy zbiór wartości posiada argument
(?)
np na tej funkcji
| | ⎧ | 2x+3 gdy x∊R\{−1,0} | |
| | ⎜ | | |
| f(x)= | ⎨ | 3 gdy x=−1 |
|
| | ⎜ | | |
| | ⎩ | 1 gdy x=0 | |
13 lis 22:42
Adamm: f: R→?
13 lis 22:47
Kamil: mój sposób na udowodnienie tego to coś w tym stylu opisowym.
wiemy że funkcja w x∊R\{−1,0} przyjmuje zbiór wartości R\{1,3}, ale wiemy że f(−1)=3 oraz
f(0)=1 czyli
funkcja przyjęła wszystkie elementy zbioru wartości.
Tylko nie wiem czy to jest dobry dowód i mi go zaliczą.
13 lis 22:56
Adamm: tu nie ma czego dowodzić
13 lis 22:58
Kamil: wiem że na pierwszy rzut oka widać że to jest suriekcja, ale muszę to jakoś udowodnić dla pana
Profesora
13 lis 22:59
Adamm: inaczej kolego bo widzę że nie rozumiesz (albo robisz sobie ze mnie jaja)
na jaki zbiór jest ta funkcja? inaczej nie ma czego rozpatrywać
funkcja jest suriekcją na jakieś zbiory, na inne już nie
13 lis 23:01
Kamil: myślałem że oczywiste że f:R→R
13 lis 23:04
Adamm: f: R → R∪{jabłko}
i co, oczywiste?
13 lis 23:06
Mila:
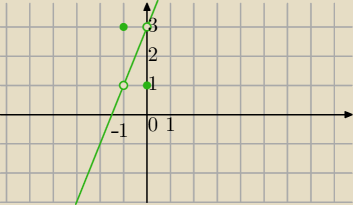
13 lis 23:09
