znalezeinie rownania bokow kwadratu kapustaglowapusta: Witam, mam pytanie czy dobrze rozumuje zadanie, poniewaz nie mam wyniku. Dany jest wierzchołek kwadrati A(2,−4) i jedna z jego przekątnych 2x−y−1=0. Znalezc rownania boków kwadratu. Robiłem to tak: Znalazłem drugą przekątną tego kwadratu, która wynosi y=−¹₂−3 Znalazłem punkt C, który wynosi (−18/5, −6/5). Środek przekątnej punkt S − (−4/5,−13/5) Jednakże chyba ten punkt C mi sie nie przyda. Rozumowałem to tak, ze jezeli obliczenie długość AS, a punkt B to (x,2x−1) to jezeli zrobie cos takiego |BS|=|AS| to mi to wyjdzie? Wyniki są tragiczne, dlatego sie pytam, chyba ze cos zle robie.

kapustaglowapusta: refresh

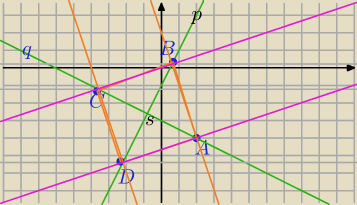
Mila: 1) A(2,−4) p: 2x−y−1=0⇔y=2x−1 A∉p 2) Przekątne są równe, prostopadłe i dzielą się na połowy.

	1		1
q: y=−		x+b, A∊q⇔−4=−		*2+b⇔b=−3
	2		2

	1
q: y=−		x−3
	2

3)

	1
Punkt przecięcia przekątnych: 2x−1=−		x−3⇔
	2

	4		13
S=(−		,−		)
	5		5

4) C: C=(x_c,y_c)

	4		2+xc		13		−4+yc
−		=		i −		=
	5		2		5		2

	18		6
C=(−		,−		)
	5		5

5) p i q proste prostopadłe

	4		13		14		−7
SA→[2+		,−4+		]=[		,		]
	5		5		5		5

	7		14
SB→⊥SA→ i wektory maja równe długości⇔SB→=[		,		]
	5		5

	4		13		7		14		4		7		13		14
S(−		,−		)→[		,		]⇒B=(−		+		,−		+		)
	5		5		5		5		5		5		5		5

	3		1
B=(		,
	5		5

	4		13		7		14		4		7		13		14
S(−		,−		)→[−		,−		]⇒B=(−		−		,−		−		)
	5		5		5		5		5		5		5		5

	11		27
D=(−		, −		)
	5		5

6)

	3		1
Prosta AB: A(2,−4),B=(		,
	5		5

y=−3x+2 prosta CD||AB ⇔ y=−3x+b i D należy do prostej⇔b=−12⇔ CD: y=−3x−12

	1
prosta CD⊥CB⇔y=		x+b i B∊prostej⇔b=0
	3

	1
y=		x
	3

prosta AD|| BC

	1
y=		x+b i A∊prostej
	3

	1
−4=		*2+b⇔b=−14/3
	3

	1		14
y=		x−
	3		3

===============

Mila: Mogła być pomyłka w danych i dlatego te rachunki takie wychodzą. Równania prostych są ładne.

Bogdan:

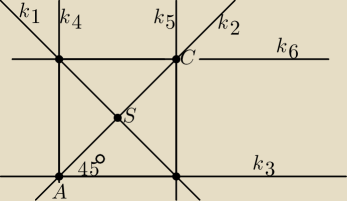
	1		1
k2: y = −		x − 3, a2 = −
	2		2

k₃: y = a₃x + b₃, k₄ = a₄x + b₄, i A∊k₃ i A∊k₄ tg45^o = 1,

	1   a3 +   2		1		1
1 = I		| ⇒ |a3 +		| = |1 −		a3|
	1   1 − a3   2		2		2

stąd a₃ = ... (są dwa rozwiązania, jedno jest równe a₃, drugie a₄)

Mila: Witaj, szkoda, że wcześniej nie napisałeś, ja zapomniałam o tym sposobie.

kapustaglowapusta: Mila, mam pytanie odnośnie tego jak znalazłaś punkt D, bo nie moge tego wykminić A przy rozwiązaniu Bogdana zgubiłem się po tym tangensie

kapustaglowapusta: Skąd się wzięło to: S(−⁴₅, −¹³₅) −> [−⁷₅,−¹⁴₁₅ −> .... i tak dalej

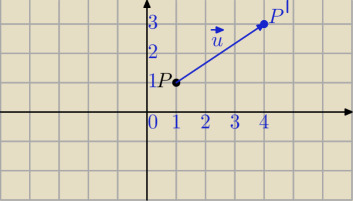
Mila: Przesunięcie punktu o wektor, P(x,y) →przesunięcie o wektor [a,b]⇒otrzymujesz punkt P'(x+a, y+b) P=(1,1) →T_u=[3,2]⇒P'(1+3,1+2)=(4,3)

Mila: Tam źle napisałam B zamiast D. Aby otrzymać punkt D bierzemy wektor przeciwny do SB ( to przecież wiesz z fizyki, jesli nawet nie było na matematyce)

	7		14
SB→=[		,		]
	5		5

wektor przeciwny:

	7		14
SD→=[−		,−		]
	5		5

	4		13		4		7		13		14
S=(−		,−		)→T[−75,−145]⇒D=(−		+(−		),−		+(−		))
	5		5		5		5		5		5

	11		27
D=(−		,−		)
	5		5

Lepszy jest sposób Bogdana, bo nie trzeba liczyć wsp. wierzchołków kwadratów. Mogę rozpisac szczegółowo.

kapustaglowapusta: To znaczy tak, ja to ogarniam Bo punkt C wiem jak zrobić, po prostu nie wiem skad wzielas wektor SD Czy to chodzi o to, ze jest on przeciwny wiec wyniki wektora SB beda o przeciwnych znakach do tego SD?

Mila: Tak wektor przeciwny do SB^→.

Mila: Dobranoc

Kapusta: Faktycznie głowa pusta

kapustaglowapusta: Okej dzieki wielkie Mila

kapustaglowapusta: Mila, ostatnie pytanko mam, dlaczego jest tak, że jeżeli chodzi o wektor prostopadły do innego wektora, dajmy na to: Wektor SA=[¹⁴₅,u−{7}{5}] to wektor przeciwny to jest [−B,A] czyli faktycznie SB = [⁷₅,¹⁴₅] A dlaczego tak samo nie mozemy zrobic z wektorem SD, przeciez on jest tez prostopadly do SA. Jednak jeżeli pomyslismy, ze wlasnie SB jest przeciwny do SD, to wyniki sie nie zgadzaja i to mnie trapi.

kapustaglowapusta: Bądź może ktoś inny wytłumaczy?

kapustaglowapusta: Tam miało być Wektor SA[....] to wektor PROSTOPADŁY**** to jest [−B,A]

Mila: Za 30 minut będę.

kapustaglowapusta: Okej, czekam

Bogdan: Tu link: https://matematykaszkolna.pl/strona/1228.html

Mila:

	14		7
SA→=[		,−		]
	5		5

	14		7		7		14
[		,−		]⊥u=[		,		] iloczyn skalarny równy 0
	5		5		5		5

	14		7		7		14
[		,−		]⊥v=[−		, −		] =−u iloczyn skalarny równy 0
	5		5		5		5

po przesunięciu S o jeden lub drugi wektor otrzymasz dwa wierzchołki, jak je nazwiesz to sprawa drugorzędna.

Mila: Witaj Bogdanie

Bogdan: Witaj Mila

kapustaglowapusta: Nie rozumiem tego dalej, rozumiem ze wektory sa prostopadłe jak iloczyn skalarny jest równy 0. Ale co mi z tego jak to widać ze faktycznie SA jest prostopadły z SB i z SD. A wektor prostopadły do wektora [A,B] to [−B,A], co by sie zgadzało z jednym wektorem, z drugim nie. Bogdan, dzieki wielkie, jutro na pewno sobie ogarne Twoj sposob

Mila: [A,B]⊥[−B,A] [A,B]⊥[B,−A]

kapustaglowapusta: To wiele wyjasnia, dzieki wielkie Mila

Mila: Rozwiąż wg wskazówek Bogdana.