zadanie z równoległobokiem..
K.m.a: W równoległoboku,w którym jeden z boków jest dwa razy dłuższy od drugiego, kąt ostry ma miarę
60o, a dłuższa przekątna ma długość 4√3.
Oblicz:
a) długości boków równoległoboku
b) objętość bryły otrzymanej w wyniku obrotu tego równoległoboku wokół dłuższego boku.
Pomocy...
30 sty 18:29
K.m.a:
30 sty 19:16
ula:

żeby obliczyc długość boków zastosuj wzór cosinusów
d
2=a
2+(2a)
2−2a*2a*cosβ
cosβ=cos(180−α)=−cosα
30 sty 19:48
K.m.a: Hmm.. widziałam gdzieś już ten sposób, aczkolwiek myślałam, że jest jakiś inny bo twierdzenie
cosinusów jest w rozszerzeniu a to zadanie ze zbioru do matury podstawowej...
No nic, nie zaszkodzi mi znać tego twierdzenia, a nóż się kiedyś przyda.
Dzięki

30 sty 19:53
K.m.a: Nadal coś nie wychodzi...

Podstawiam:
(4
√3)
2 = a
2 + (2a)
2 − 2*a*2a*cosβ
cosβ = cos120
o = −0,5
48 = a
2 + 4a
2 − 4a
2 * (−0,5)
48 = a
2 + 4a
2 + 2a
2
48 = 7a
2 ....
a w odpowiedziach mam że boki są 4 i 8...
gdzie jest błąd? bo z powyższego nie wyjdzie a = 4...

30 sty 20:09
ula:
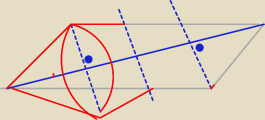
z b będzie trochę gorzej, nie wiadomo o jaki obrót tu chodzi
Jakbyś obracał tylko Δ(a,d,2a) to by były 2 ostrosłupy
Obracamy jednak 2 Δ różnie położone i tu jest problem
powstaje skąplikowana figura
czrwony to 1/2 tej figury
Powstają 2 takie same stożki oraz 2 takie same stożki ścięte
30 sty 20:09
ula: słuchaj może przekątna ma długość 4√7 nie √3 to by wyszło dobrze
30 sty 20:17
30 sty 20:22
K.m.a: właśnie już sprawdzałam... i mam 4
√3 
30 sty 20:22
K.m.a: tak, to będzie ten walec, bo biorąc pod uwagę boki z odpowiedzi, wychodzi dobra objętość..
tylko te nieszczęsne boki...
30 sty 20:24
ula: masz rację, źle przeczytałam zadanie
30 sty 20:25
 żeby obliczyc długość boków zastosuj wzór cosinusów
d2=a2+(2a)2−2a*2a*cosβ
cosβ=cos(180−α)=−cosα
żeby obliczyc długość boków zastosuj wzór cosinusów
d2=a2+(2a)2−2a*2a*cosβ
cosβ=cos(180−α)=−cosα

 Podstawiam:
(4√3)2 = a2 + (2a)2 − 2*a*2a*cosβ
cosβ = cos120o = −0,5
48 = a2 + 4a2 − 4a2 * (−0,5)
48 = a2 + 4a2 + 2a2
48 = 7a2 ....
a w odpowiedziach mam że boki są 4 i 8...
gdzie jest błąd? bo z powyższego nie wyjdzie a = 4...
Podstawiam:
(4√3)2 = a2 + (2a)2 − 2*a*2a*cosβ
cosβ = cos120o = −0,5
48 = a2 + 4a2 − 4a2 * (−0,5)
48 = a2 + 4a2 + 2a2
48 = 7a2 ....
a w odpowiedziach mam że boki są 4 i 8...
gdzie jest błąd? bo z powyższego nie wyjdzie a = 4... 
 z b będzie trochę gorzej, nie wiadomo o jaki obrót tu chodzi
Jakbyś obracał tylko Δ(a,d,2a) to by były 2 ostrosłupy
Obracamy jednak 2 Δ różnie położone i tu jest problem
powstaje skąplikowana figura
czrwony to 1/2 tej figury
Powstają 2 takie same stożki oraz 2 takie same stożki ścięte
z b będzie trochę gorzej, nie wiadomo o jaki obrót tu chodzi
Jakbyś obracał tylko Δ(a,d,2a) to by były 2 ostrosłupy
Obracamy jednak 2 Δ różnie położone i tu jest problem
powstaje skąplikowana figura
czrwony to 1/2 tej figury
Powstają 2 takie same stożki oraz 2 takie same stożki ścięte
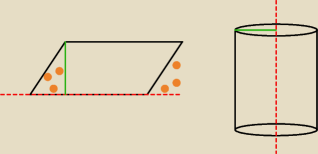 A ta bryła to nie będzie po prostu walec? z jednej strony jest ten stożek, z drugiej sie wcina,
zostanei sam walec. a promień podstawy to bedzie ta wysokość zielona? tylko najpierw trzeba
boki obliczyć
A ta bryła to nie będzie po prostu walec? z jednej strony jest ten stożek, z drugiej sie wcina,
zostanei sam walec. a promień podstawy to bedzie ta wysokość zielona? tylko najpierw trzeba
boki obliczyć

