Analityczna Aga: Wyznacz równanie prostych, w których zawierają się dwusieczne kątów, pod jakimi przecinają się proste k: 4x+2y+1=0 i m: 11x−2y+7=0.

	8		17
Znalazłam punkt przecięcia prostych P( −		,		) i nie wiem jak znaleźć Q, czyli
	15		30

punkt równoodległy od prostych.

5-latek: Dwusieczna kąta to miejsce geometryczne punktow ktore sa rownoodleglege od ramaion kata Wiec

|Ax0+By0+C|		|A1x0+B1y0+C1|
	=
√A2+B2		√A12+B12

prosta k A=4 B=2 C=1 prosta m A₁= 11 B₁= −2 C₁= 7

|4x0+2y0+1|		|11x0−2y0+7|
	=
√20		√125

to rozwiazac i masz te rownania

Aga: Ok, ale tu mam dwie niewiadome w jednym równaniu Jak to rozwiązać?

5-latek: Po pomnozeniu obu stron przez √20*√125 (wtedy pozbedziemy sie mianownikow bedzie √125|4x₀+2y₀+1|= √20|11x₀−2y₀+7| 5√5|4x₀+2y₀+1|= 2√5|11x₀−2y₀+7}| teraz |x|= |y|⇔x=y lub x=−y 5√5(4x₀+2y₀+1)= 2√5(11x₀−2y+0+7) Rozwiqz to i napisz rownanie dwusiecznej w postaci ogolnej tylko napisz bex tego x₀ i y₀ tylko Ax+bY+c 5√5(4x₀+2y₀+1)= −2√5(11x₀−2y₀+7) tak samo tylko opuci te indeksy 0 przy x₀ i y₀

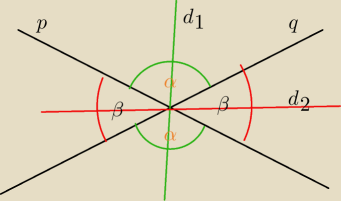
5-latek: Zeby bylo wiadomo o czym mowimy to jesli mamy dwie przecinajace sie proste p i q to tworza one dwie pary katow wierzcholkowych wiec beda dwie dwusieczne

Aga: Ok, dzięki, teraz już mi wyszło. Już rozumiem