Funkcje różniczkowalne Mariusz: Dobry wieczór. Mam dwa zdanka Wykazać ,że ∀a,b∍R+ : a<b ⇒ b−a/b<ln b/a<b−a/a oraz Wykazać ,że ∀x∍[0,1]: x ≤ arcsinx≤ x/sqrt(1−x²) Wydaje mi się że trzeba skorzystać z tw. Rolle'a ale nie wiem jak to ruszyć byłbym wdzięczny za jakąś podpowiedź lub zrobienie/wytłumaczenie jednego zadania. Wtedy mam nadzieje poradzę sobie z kolejnym. Z góry dziękuje za pomoc

kochanus_niepospolitus: jak już to : a,b ∊ R₊

jc: Na pewno a < b ⇒ ln b/a < b − 1 ? a=1/3, b=1, ln 3 < 0 ? raczej nie.

kochanus_niepospolitus:

	a		b		a
tam masz b −		< ln		< b −		Bo chyba nie ... tak trudno napisać
	b		a		a

nawiasy

kochanus_niepospolitus: Studenta uczą tw. Rolle'a a nawet poprawnie zapisać ułamków nie potrafi.

Mariusz: kochanus_niepospolitus: wybacz nie mogłem znaleźć tego znaku a był pod nosem a co do nawiasów (b−a)/b<ln b/a <(b−a)/a

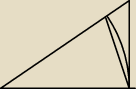
jc: 0 ≤ x ≤ 1 ⇒ x ≤ arcsin x ≤ x/√1−x² x=sin t, 0≤t≤π/2 sin t ≤ t ≤ tg t faktycznie tak jest, odczytujesz to z rysunku. Podstawa = 1, pole małego trójkąta ≤ pole wycinka ≤ pole dużego trójkąta

kochanus_niepospolitus: Mariusz −−− ale ja pisząc te słowa miałem na myśli brak NAWIASÓW