uklad rownan Blee: Witam! Były ktoś w stanie rozwiązać ten układ równań? Męczę się z nim cały dzień i nic kompletnie nie wychodzi. Proszę o pomoc!

⎧	2y + x2 − 6x + 2 = 0
⎩	x2 + y2 + 2x − 4y − 5 = 0

5-latek: Moze byc niemilo jak to zobaczy prawdziwy Blee

Blee: Ale ja się pod nikogo nie podszywam i nawet nie śmiem wątpić że jestem jakimś Blee. W przypływie kreatywności wymyśliłam byle jaką nazwę. Zależy mi jedynie na tym zadaniu; nie mam zamiaru z nikim wchodzić w konflikty. Pozdrawiam serdecznie

Blee: *nie śmiem twierdzić

Blee("fałszywy"): To jak? Mogę liczyć na jakąś pomoc?

Milo: Próbowałeś po prostu wyznaczyć y z pierwszego równania i wstawić do drugiego? Wyjdzie wielomian 4 stopnia, ale może ładny?

5-latek: Mozna to rozwiazc graficznie Pierwsze rownanie to rownanie paraboli

	1		1
2y= −x2+6x−1 ⇒y= −		x2+3x−
	2		2

Drugie rownanie to rownanie okregu (x+1)²+(y−2)²=10

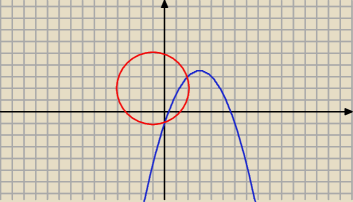
Adamm: (x+1)²+(y−2)²=10 x=0, y=−1 x=2, y=3

Blee(fałszywy): Odjęłam od siebie równania i następnie wyznaczyłam x i podstawiłam do pierwszego równania. Wychodziły mi "igreki" do potęgi 4, 3, 2... o ile z potęgą 4 i 2 bym sobie poradziła, o tyle z tymi do 3 nie wiedziałam co zrobić.

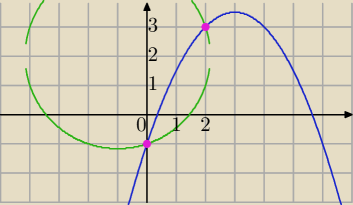
Mila:

	1
x2 − 6x +2y+ 2 = 0 ⇔y=−		x2+3x−1
	2

x² +2x+ y² − 4y − 5 = 0 ⇔(x+1)²−1+(y−2)²−4−5=0⇔(x+1)²+(y−2)²=10 ============= graficznie: (0,−1), (2,3) 2) algebraicznie:

	1
y=−		x2+3x−1 podstawiamy do (2) równania:
	2

	1
(x+1)2+(−		x2+3x−1−2)2=10
	2

	1
(x+1)2+(−		x2+3x−3)2=10
	2

	1		1		1
x2+2x+1+		x4+9x2+9+2*(−		x2*3x)+2*(−		x2*(−3)+2*3x*(−3)−10=0⇔
	4		2		2

1
	x4−3x3+13x2−16x=0
4

	1
x*(		x3−3x2+13x−16)=0
	4

	1
x=0 lub (		x3−3x2+13x−16)=0
	4

x=0 to y=−1 lub

	1
(		x3−3x2+13x−16)=0
	4

	1
W(2)=		*8−3*4+13*2−16=2−12+26−16=0
	4

	1
x=2 to y=−		*4+3*2−1=−2+6−1=3
	2

Na podstawie metody graficznej ( nawet mało dokładnego szkicu) mamy dwa rozwiązania, ale możesz wykonać dzielenie

	1
(		x3−3x2+13x−16):(x−2)
	4

Blee(fałszywy): Dziękuje bardzo Wam wszystkim! Co prawda wielomianów jeszcze nie miałam, ale z Waszą pomocą jakoś mi się udało dojść do rozwiązania. Dobrej nocy życzę

5-latek: Wez gosciu nie griluj

Blee(fałszywy): To już cieszyć się nie można?