grupy
algebra:
D
3−grupa wszystkich izometrii wlasnych trojkata rownobocznego.
|D
3|=2*3=6.
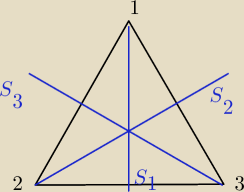
Na rysunku: trojkat rownoboczny o wierzcholkach 1, 2, 3.
Osie symetrii tak jak na rysunku.
Przeksztalcaja one wierzcholki trojkata nastepujaco:
S
1(1)=1
S
1(2)=3
S
1(3)=2
S
2(1)=3
S
2(2)=2
S
2(3)=1
S
3(1)=2
S
3(2)=1
S
3(3)=3
O−obrot (w kierunku przeciwnym do ruchu wskazowek zegara)
O
0− obrot o 0
o. Jest to element neutralny.
O
0(1)=1
O
0(2)=2
O
0(3)=3
Jak beda przeksztalcac wierzcholki obroty o 120
o i 240
o (nie umiem tego zobaczyc)?
 D3−grupa wszystkich izometrii wlasnych trojkata rownobocznego.
|D3|=2*3=6.
Na rysunku: trojkat rownoboczny o wierzcholkach 1, 2, 3.
Osie symetrii tak jak na rysunku.
Przeksztalcaja one wierzcholki trojkata nastepujaco:
S1(1)=1
S1(2)=3
S1(3)=2
S2(1)=3
S2(2)=2
S2(3)=1
S3(1)=2
S3(2)=1
S3(3)=3
O−obrot (w kierunku przeciwnym do ruchu wskazowek zegara)
O0− obrot o 0o. Jest to element neutralny.
O0(1)=1
O0(2)=2
O0(3)=3
Jak beda przeksztalcac wierzcholki obroty o 120o i 240o (nie umiem tego zobaczyc)?
D3−grupa wszystkich izometrii wlasnych trojkata rownobocznego.
|D3|=2*3=6.
Na rysunku: trojkat rownoboczny o wierzcholkach 1, 2, 3.
Osie symetrii tak jak na rysunku.
Przeksztalcaja one wierzcholki trojkata nastepujaco:
S1(1)=1
S1(2)=3
S1(3)=2
S2(1)=3
S2(2)=2
S2(3)=1
S3(1)=2
S3(2)=1
S3(3)=3
O−obrot (w kierunku przeciwnym do ruchu wskazowek zegara)
O0− obrot o 0o. Jest to element neutralny.
O0(1)=1
O0(2)=2
O0(3)=3
Jak beda przeksztalcac wierzcholki obroty o 120o i 240o (nie umiem tego zobaczyc)?