tryg ja: rozwiąż nierówność 4cos⁴ t −7cos²t+4>0 i zilustruj rozwiązanie na okręgu x²+y²=1

ja: proszę o wskazówki

jc: x = cos t, y = sin t x²+y²=1 4x⁴ − 7x² +4 = 4(x²−1)² + x² > 0 zawsze rozwiązaniem jest cały okrąg

ja: czy za x można podstawić t? Trochę jestem laikiem jeśli chodzi o ten typ zadań. Zastanawia mnie czy nie rozwiązuje się najpierw nierówności ze względu na t a dopiero potem ten końcowy element z którym nie mogę sobie poradzić .

PW: Po podstawieniu cost=x otrzymujesz nierówność (1) 4(x²−1)² + x² > 0, która jest prawdziwa dla wszystkich x∊R. Ponieważ wcześniej podstawiliśmy x=cost, oznacza to że nierówność jest prawdziwa "dla każdego kosinusa" − dla każdej liczby t.. Taka powinna być odpowiedź . O co chodzi z tym "przedstawieniem rozwiązania na okręgu"? Jak można przedstawić zbiór liczb rzeczywistych na okręgu? Jest to całe zadanie, czy fragment czegoś większego, czego nie napisałeś?

ja: Zadanie brzmi: rozwiąż nierówność.Zilustruj jej rozwiązanie na okręgu x²+y²=1

PW: No dobrze. A gdyby zadanie brzmiało: Rozwiąż nierówność t²+t+1 > 0 i zilustruj jej rozwiązanie na okręgu x²+y²=1, to wiedziałbyś o co chodzi?

ja: Z rozwiązanim nierówności kłopotu nie ma będzie zbiór R ale jak to przenieść na okrąg nie mam zielonego pojęcia

PW: Ja też nie. Może jeszcze raz zajrzy tu jc, który nie miał wątpliwości.

jc: punkty x= cos t, y = sin t leżą na okręgu x²+y²=1. Gdyby nierówność opisywała jakiś obszar, to patrzylibyśmy na część wspólną, ale zbiór rozwiązań nierówności jest pusty. Oczywiście w nierówności należałoby zamienić cos t i sin t na x, y.

PW: Kurde, nierówność jest jednej zmiennej. Jak można jej rozwiązanie ilustrować na okręgu? To jakieś "dłubanie w uchu".

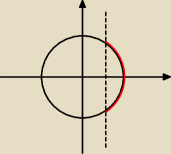
jc: Można x ≥ 1/2 x²+y² Czyli mamy kąty od −60^o do 60^o.

jc: Miało być x²_y²=1. W tym zadaniu nie widać większych korzyści, ale nawet w takim zadaniu wolę odczytywać kąty z rysunku.

jc: Znów coś się zgubiło. x²+y²=1.

PW: Sądzę, że niejaki ja podpuszcza nas. 361337

ja: nie podpuszczam zadanie 361337 nie należy do mnie. mam całą listę tych nierówności i wszystkie są do zilustrowania na okręgu np 8sin⁴−10sin²+3<0

PW: Marudzisz. Ten ostatni zapis nie ma sensu.

ja: tak przepraszam 8sin⁴t−10sin²t+3<0

PW: Zgodzę się, jeżeli polecenie będzie brzmiało tak: Punkty (x,y)=(sint,cost) należą do okręgu jednostkowego. Wskaż takie, których współrzędne spełniają nierówność 8sin²t−10sin²+3<0. Tyle że w ten sposób uprawiasz geometrię analityczną, a nie trygonometrię, jak podałeś w temacie pierszego postu.

ja: zadania są z działu trygonometria

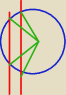
PW: 8sin⁴t−10sin²t + 3 > 0 Δ=100−96=4

	3		1
x1=−		, x2=−
	4		2

	3		1
x<−		lub x >−
	4		2

	3
Skoro iksy (czyli sin2t )mają być mniejsze od −		, to znaczy że rozwiązaniami są kąty
	4

t należące do zakresu pokazanego przez "pierwszy z lewej zielony kąt". Te x (czyli

	1
sin2t) , które mają być większe niż −		pokazują kąty będące drugą częścią rozwiązania
	2

(kąty należące do obszaru wyznaczonego przez "prawy zielony wklęsły" kąt. Zamiast wyliczać dokładnie jakie to są kąty t, wskazujemy je jako kąty z pewnego zakresu na rysunku, ale przecie do licha te kąty (czyli rozwiązania nierówności) nie należą do okręgu. Polecenie jest tylko dla tych, co to "ty wiesz, a ja rozumiem".

PW: Tfu, jeszcze źle zrobiłem. Należało oznaczyć y=sin²t (bo to sinusy) i wtedy inny będzie rysunek − oś OY przecinamy prostymi y=−3/4 lub y=−1/2 i zaznaczamy odpowiednie obszary dla kąta t.

ja: a dlaczego y=−3/4 lub y=−1/2 ?

PW: Bo się pomyliłem przy liczeniu w pamięci (przy pisaniu on line z ekranu znika treść zadania i wziąłem +10 zamiast −10) √Δ = 2, a więc

	10−2		1		10+2		3
y1 =		=		, y2=		=
	2.8		2		16		4

i nasze sin²t musi być mniejsze od 1/2 lub większe od 3/4. Jest to pechowe zadanie, cały czas się mylę, ale już wiesz o co idzie, a i ja się czegoś nauczyłem.

ja: przez cały dzień chodziło mi to zadanie po głowie i już wydaje mi się że wiem o co chodzi dziękuję za poświęcony czas