równanie xc: Wyznacz wszystkie wartości parametru k dla których równanie x⁴−40x²+k=0 ma rozwiązania tworzące ciąg arytmetyczny Dla wyznaczonej wartości k podaj te rozwiązania Proszę o pomoc

PW: Dla k=0 mamy równanie x⁴−40x² = 0 x²(x²−40)−0, którego rozwiązaniami są −√40, 0, √40 − trzy liczby tworzące ciąg arytmetyczny o różnicy √40, Myślimy dalej?

PW: x⁴−40x²+20²−20²+k = 0 (x²−20)² = 400−k Dla jakich k na pewno nie ma żadnych rozwiązań?

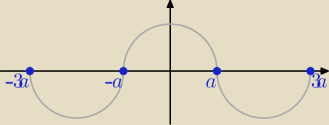
Eta: No to teraz tak dla k≠0 rozwiązania układają się symetrycznie na osi Ox ( dlaczego tak ? ..... pomyśl sam/a to: (x−3a)(x+3a)(x−a)(x+a)=0 (x²−9a²)(x²−a²)=0 x⁴−10a²x²+9a⁴=0 k=9a⁴ i −10a²=−40 ⇒ a²=4 to k=9*16=144 i mamy równanie (x²−36)(x²−4)=0 x=−6v x=6 v x=2 v x= −2 ====================== −6,−2,2,6 −−− tworzą ciąg arytmetyczny Odp: k=0 ( co podał PW lub k=144 ( co podaję ja

PW: Eta − mam pytanie. Czy istniejące dla k=400 dwa rozwiązania uczeń ma potraktować jako spełniające warunki zadania? Formalnie każde dwie liczby spełniają definicję ciągu arytmetycznego (dwuwyrazoego).

Eta: Aby ciąg był arytmetyczny muszą być dane 3 kolejne wyrazy!

PW: O to pytam − czy w szkolnej definicji zakłada się, że ciąg arytmetyczny musi mieć co najmniej 3 wyrazy?

Eta: Tak , taka jest definicja ...."co najmniej trzy kolejne wyrazy"

Eta: A "autor posta" i tak ma to głęboko w ...........

PW: Dziękuję, dawno nie miałem w rękach żadnego podręcznika do średniej szkoły.

'Leszek: Dla kazdej liczby n ε N₊ , a_n+1 − a_n = r , r = const.

Eta: Na zdrowie

Eta: 2,4,8,10, −−−− czy tworzą ciąg arytmetyczny?

Kacper: Trzeba by się zastanowić, czy dwie liczby tworzą w ogóle jakiś ciąg?

PW: Oczywiście. W zadaniach z kombinatoryki nikt nie ma wątpliwości, że opisując rzut dwiema kostkami tworzymy model z dwuwyrazowych ciągów (1,1),(1,2), itd.

kacper: witam mam problem z tą częścią zadania: rozwiązania układają się symetrycznie na osi Ox ( dlaczego tak ? ..... pomyśl sam/a (wydaje mi się że jest to spowodowane podwójną deltą, dlatego są symetrycznie na osi) nie rozumiem czemu tam się znalazły właśnie −3a,−a,a,3a: dlaczego nie inne parametry?

PW: Nieśmiertelna delta, i to jeszcze "podwójna". Nie zależy to od żadnej delty. Po prostu, wielomian po lewej stronie jest funkcją parzystą, W(−x)=W(x) dla dowolnych x∊R. Jeżeli liczba a jest jego pierwiastkiem, czyli W(a)=0, to także W(−a)=0. Stąd pierwiastki są "symetrycznie na osi". Jeżeli dla a>0 liczby −a oraz a są kolejnymi w ciągu arytmetycznym pierwiastkami, to różnica tego ciągu jest równa r = a−(−a) = 2a, dlatego następny pierwiastek po a musi być równy a+2a=3a. Warto się uczyć od Ety.

Eta: