styczna Maciek: f(x)=ax³+bx²+cx+d y₁=2−x y₂=2x wyznacz a, b, c, d wiedząc, że funkcja f(x) jest styczna do funkcji y₁ oraz funkcji y₂ na wysokości y=2

kochanus_niepospolitus: y₁: skoro ma być styczna do f(x) to będzie to w punkcie: 2 = 2 − x −> x= 0 y₂: analogicznie: 2 = 2x −> x=1 więc mamy: f(0) = 2 −> d = 2 (pierwsze równanie) f(1) = 2 −> a + b + c = 0 (drugie równanie) wzór na styczną f(x) w punkcie x=0 = y₁ (trzecie równanie) wzór na styczną f(x) w punkcie x=1 = y₂ (czwarte równanie) Masz cztery równania, cztery niewiadome. Rozwiązujesz

Maciek: wychodzi x³−x+2?

Jerzy: Sprawdzimy: x₀ = 2 f'(x) = 3x² − 1 f'(2) = 12 − 1 = 11 f(2) = 8 y = f'(2)(x − 2) + f(2) = 11(x − 2) + 8 = 11x − 14 ≠ 2 − x

kochanus_niepospolitus: Jerzy ... czemu x₀=2

kochanus_niepospolitus: to y=2 przecież

Jerzy: No bo dla mnie: 2 = 2 − x ⇔ x = 2

kochanus_niepospolitus: no ... można i tak

kochanus_niepospolitus: Maciek − dobrze Ci wyszło

Maciek: Ale to czemu to jest "styczna" skoro przecina jeszcze y₂ dla x=−2

Jerzy: Masz przecież dwie styczne.

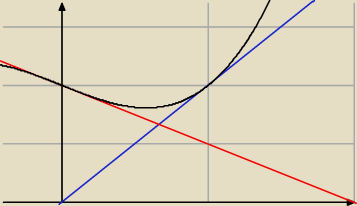
kochanus_niepospolitus: Jak widzisz ... 'pasuje'. Prosta jest styczna do krzywej f(x) to nie oznacza, że jej 'nie przebija' w punkcie styczności (patrz x₀=0)

Adamm: x=0, y=2, y=2−x x=1, y=2, y=2x i mamy tak f'(x)=3ax²+2bx+c d=2 a+b+c+d=2 c=−1 3a+2b+c=2 układ 4 równań

Adamm: i faktycznie, f(x)=x³−x+2

Adamm: styczna, bo ma takie samo nachylenie do osi OX jak funkcja w tym punkcie

Maciek: nachylenie funkcji w punkcie?

Adamm: tak nachylenie funkcji w punkcie

Eta: @Adamm Od kiedy "funkcja" ma "nachylenie" ?

Adamm: nachylenie wykresu funkcji ok?

Eta: Teraz ok