Znowu problem taki ogólny ze stereometrii MatMal: Powiedzmy ze mamy ostroslup, i jesli mam zmierzyc kat miedzy dwiema plaszyznami, plaszczyzna boczna i plaszczyzna podstawy, to tak generalnie musze wziac wysokosc sciany bocznej i odcinek padajacy w ten sam pkt pod katem prostym w podstawie ? i Zmierzyc kat miedzy nimi ? Czy niezaleznie ktore proste wybiore z obu plaszczyzn to i tak kat miedzy nimi bedzie taki sam ?

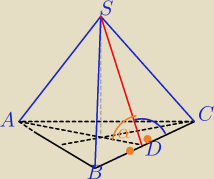
Mila: AD⊥BC SD⊥BC α− kąt między ścianą boczną płaszczyzną podstawy.

MatMal: no niby tak, tylko w zadaniu czasem nie da sie wywnioskowac ze ktorac z tych prostych jest pod katem prostym ... i dlatego moje pytanie

Mila: Napisz konkretne zadanie, pisał Ci PW jaka jest zasada.

MatMal: Podstawą ostrosłupa jest trapez prostokątny,którego podstawy mają długość 3 cm i 6 cm,a ramiona 4 cm i 5 cm.Wszystkie ściany boczne są nachylone do płaszczyzny podstawy pod tym samym kątem ostrym miary \alpha .Wyznacz sinus kąta \alpha ,jeśli wysokość ostrosłupa jest równa 6 cm. oczywiscie wiem, wnioskuje ze spodek jest w srodku okregu wpisanego, r=2 az sie prosi o pitagorasa, w trojkacie H r h (H wysokosc ostroslupa , r promien okrego wpisanego h wysokosc sciany bocznej) i tu pojawia sie moje pytanie skad mam wiedziec ze wysokosc tej sciany bocznej opadnie w to samo miejsce w ktorego opada promien okgregu wpisanego ( nie pytam jak cos o roziwaznaie zadania bo ono jest proste, tylko mnie nurtuje ten problem i chyba tego nie rozumiem xD)

PW: Chcesz przeciąć krawędź podstawy płaszczyzną prostopadłą. Wiesz, że wysokość ściany bocznej jest prostopadła do krawędzi podstawy. Wiesz, że promień okręgu jest prostopadły do krawędzi podstawy (w punkcie styczności). Punkt styczności w trapezie prostokątnym jest środkiem ramienia prostopadłego do podstawy. Pośrodku tego ramienia jest więc punkt , przez który przechodzą dwie prostopadłe do krawędzi podstawy. Na mocy twierdzenia o trzech prostopadłych płaszczyzna wyznaczona przez te proste jest prostopadła do krawędzi podstawy,.Na tej płaszczyźnie mierzy się więc kąt α nachylenia ściany bocznej do podstawy. Tłumaczenie tego jest jak widzisz zawiłe (nieosiągalne dla większości uczniów). Dlatego poprzestajemy na zaznaczeniu kropeczkami odpowiednich kątów prostych − jak to zrobiła Mila − zakładając, że czytelnik obeznany z twierdzeniem o trzech prostopadłych i definicją kąta między płaszczyznami wie o co idzie. Ty już wiesz, bo jesteś dociekliwy. Dla pocieszenia dodam, że nikt na maturze nie wymaga pisemnego tłumaczenia, dlaczego akutar tutaj jest kąt między płaszczyznami − wystarczy dobrze narysować.