geometria analityczna zobacz podgląd: Podaj interpretację geometryczną układu nierówności:

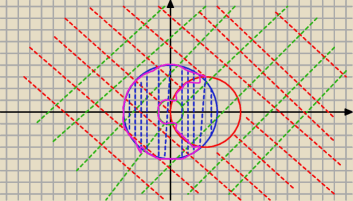
⎧	x2 + y2 ≤ 16
⎨	x2 + y2 − 6x ≥ 0
⎩	x2 + y2 ≥ 1

kochanus_niepospolitus: 1) koło o środku w S(0,0) i r = 4 2) przestrzeń bez wnętrza okręgu o środku w S(0,3) i r = 3 3) przestrzeń bez wnętrza okręgu o środku w S(0,0) i r = 1 Jesteś w stanie to narysować PS. (1) i (3) równanie dają w sumie 'oring' o środku w S(0,0) i promieniach r=1 i R=4 ... wyrzucasz z tego co nie spełnia (2) równania i masz gotowe

piotr: WRZOSOWY KSIĘŻYC

zobacz podgląd: hmmm, spróbuję

zobacz podgląd: kurde jak ja tego wszystkiego nie ogarniam,... możecie polecić jakieś stronki albo książki do nauki matmy czy coś? z góry dzięki

Adamm: wrzosowy księżyc

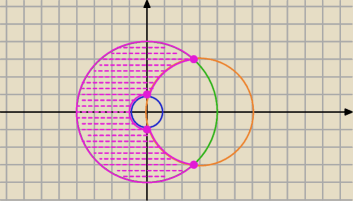Mila: x² + y² − 6x ≥ 0 ⇔ (x−3)²−9+y²≥0⇔ (x−3)²+y²≥3² x² + y² ≤ 16, ,x² + y² ≥ 1