Funckja kwadratowa Mysiasty54: Jak obliczyć pole trójkąta o punktach A(−1,2) B(3,3) oraz C(2,7)? Mam jakiś wzór, ale jest podobno jakiś sposób by liczyć trójkami czy coś(słyszałem).

Puma23: jest kilka sposobow liczenia pola trojkata jesli masz wzor to licz .

Oliwia : Ja zrobiłabym to wektorami i wyliczyła tym samym d później wyloczyłabym boki ze wzoru na odległość punktów podstawiła do wzoru i odpowiedz gotowa

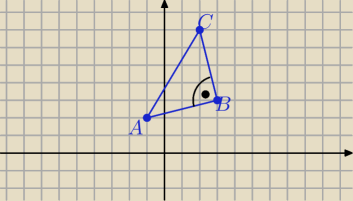
Eta: Trójkąt ABC jest prostokątny i równoramienny ( sprawdź to) |AB|=|BC|= √17

	1
P=		*√17*√17= ..............
	2

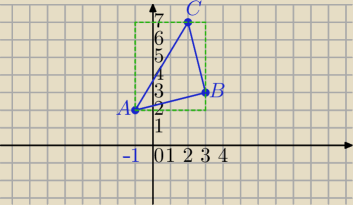
Mila: I ) sposób na poziomie SP

	1		1		1
PΔABC=4*5−(		*4*1+		*4*1+		*3*5)=8.5
	2		2		2

II) sposób− wektory i wyznacznik AB^→=[4,1] AC^→=[3,5]

	1		1
PΔ=		*|4*5−1*3|=		*17=8.5
	2		2

III) sposób− Badasz czy Δ jest prostokątny |AB|=√4²+1²=√17 |AC|=√3²+5²=√34 |BC|=√1²+4²=√17 |AC|²=34 |AB|²+|BC|²=17+17=34⇔ΔABC− Δprostokątny

	1		17
PΔ=		*√17*√17=		=8.5
	2		2

Mysiasty54: Dziękuję za pomoc. Wykorzystam chyba sposób z wektorami.

Adamm: czwarty sposób, iloczyn wektorowy a=[4; 1; 0] b=[3; 5; 0] axb=[0; 0; 17]

	1
P=		|axb|=17/2
	2

Mysiasty54: A ta 5 w AC oraz 4 w AB skąd się wzięły?

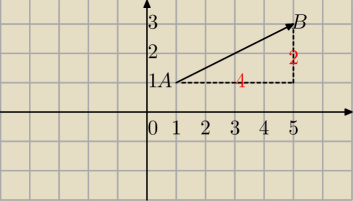
Mila: AB^→[4,2] odczytuję w tak prostych przypadkach Albo liczysz tak: A(1,1) B(5,3) AB^→=[5−1,3−1]=[4,2]