Nierówności
aalicjaa1306: Rozwiąż nierówności:
2x > exp x
2 < |e2x −3| < 3
exp (−x) ≤ x5 + 1
7 lis 19:55
Sqrti:
2x > exp(x)
2x > ex
2 > e ⇒ sprzeczność
2 < |e2x − 3| < 3
2 < |e2x − 3| i |e2x − 3| < 3
( 2 < e2x − 3 lub −2 > e2x − 3 ) i ( e2x − 3 < 3 i e2x − 3 > −3 )
( ln(√5) < x lub ln(1) > x ) i ( x < ln(√6) i e2x > 0 )
e2x > 0 dla x ∊ R
więc ostatecznie :
( ln(√5) < x lub ln(1) > x ) i x < ln(√6)
x ∊ ( −∞, 0 ) suma ( ln(√5), ln(√6)
exp(−x) ≤ x5 + 1
e−x ≤ x5 + 1
5√e−x − 1 ≤ x
5√e−x − 1 = x ⇒ x = 0
teraz sprawdzamy znaki lewej i prawej strony
5√e−x − 1 > 0
e−x > 1
−x > ln(1)
−x > 0
x < 0
5√e−x − 1 ≤ x
Lewa strona nierówności jest dodatnia dla x < 0, a prawa dla x > 0.
Z tego wynika, że prawa będzie większa dla x > 0 plus jeszcze 5√e−x − 1 = x ⇒ x = 0,
więc mamy zakres x ∊ ( 0,∞)
7 lis 20:55
Adamm:
2
x>e
x
(e/2)
0>(e/2)
x
0>x
2<|e
2x−3|<3
t=e
3x>0
2<|t−3|<3
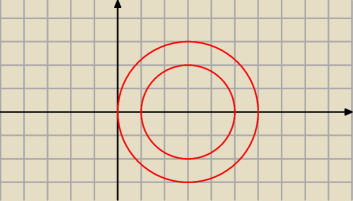
żeby się nie męczyć z przedziałami, rysujemy sobie okrąg (łatwiej się pracuje na płaszczyźnie
niż na prostej, jest bardziej obrazowo)
t∊(0;1)∪(5;6)
e
2x<e
0 lub e
ln5<e
2x<e
ln6
x<0 lub (1/2)ln5<x<(1/2)ln6
e
−x≤x
5+1
dla x<0 mamy e
−x>1>x
5+1
dla x=0 mamy e
−x=x
5+1
dla x>0 mamy e
−x<1<x
5+1
zatem x=0
7 lis 21:02
 2x>ex
(e/2)0>(e/2)x
0>x
2<|e2x−3|<3
t=e3x>0
2<|t−3|<3
żeby się nie męczyć z przedziałami, rysujemy sobie okrąg (łatwiej się pracuje na płaszczyźnie
niż na prostej, jest bardziej obrazowo)
t∊(0;1)∪(5;6)
e2x<e0 lub eln5<e2x<eln6
x<0 lub (1/2)ln5<x<(1/2)ln6
e−x≤x5+1
dla x<0 mamy e−x>1>x5+1
dla x=0 mamy e−x=x5+1
dla x>0 mamy e−x<1<x5+1
zatem x=0
2x>ex
(e/2)0>(e/2)x
0>x
2<|e2x−3|<3
t=e3x>0
2<|t−3|<3
żeby się nie męczyć z przedziałami, rysujemy sobie okrąg (łatwiej się pracuje na płaszczyźnie
niż na prostej, jest bardziej obrazowo)
t∊(0;1)∪(5;6)
e2x<e0 lub eln5<e2x<eln6
x<0 lub (1/2)ln5<x<(1/2)ln6
e−x≤x5+1
dla x<0 mamy e−x>1>x5+1
dla x=0 mamy e−x=x5+1
dla x>0 mamy e−x<1<x5+1
zatem x=0